Поле заряда, расположенного под границей двух диэлектриков

Рассмотрим случай экранировки зарядов на рисунке 3.24. Заряд q ₀ расположен в среде I с диэлектрической постоянной ε = ε ₁. Требуется найти поле, создаваемое зарядом q ₀ в среде II с диэлектрической постоянной ε = ε ₂. Оказывается, что в общем случае невозможно подобрать систему зарядов, которые бы давали одновременно правильное значение поля и потенциала одновременно в обеих средах I и II. Поэтому поле в среде I будем искать как поле двух зарядов q ₁ и q ₂, а поле в среде II – как поле заряда q ₃, расположенного в той же точке, что и заряд q ₁. Конечно, физически существует только заряд q ₀, поле и потенциалы в средах I и II получаются из-за поляризации диэлектриков. Однако оказывается, что подход с введением фиктивных зарядов q ₁, q ₂ и q ₃ удобен и позволяет правильно рассчитывать распределение полей и потенциалов в сложных слоистых системах. Выберем величину заряда q ₂ = - αq ₁, разницу в величинах ε ₁, ε ₂ включим в множитель α. Тогда получим выражения для нормальной (E _n) и тангенциальной (E _τ) составляющих электрического поля, изображенных на рисунке 3.24.

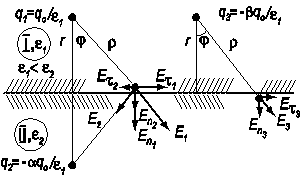
Рис. 3.24. Схема, поясняющая экранировку зарядов границей раздела двух диэлектриков

Сверху границы в области I, где поле определяется зарядами q ₁ и q ₂, находящимися на на расстоянии τ от границы в среде с диэлектрической проницаемостью ε ₁,

,

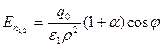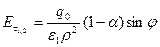. (3.137)

Снизу границы в области II, где поле определяется зарядом q ₃ в среде с ε ₁,

,

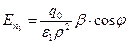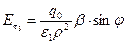. (3.138)

Используя условие постоянства на границе двух диэлектрических сред тангенциальной составляющей напряженности электрического поля и нормальной составляющей индукции электрического поля 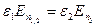, получаем:

,

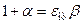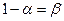, (3.139)

где .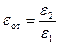

Отсюда следует, что

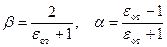. (3.140)

Таким образом, для правильного рассмотрения электрического поля и потенциала, создаваемого зарядом q ₀ в среде I с ε ₁ и находящегося под границей со средой II с ε ₂, необходимо при расчете поля в среде I с диэлектрической постоянной ε ₁ пользоваться зарядами q ₁ и q ₂, расположенными равноудаленно от границы раздела. Величина q ₂ = - αq ₁, где α приведена в (3.140). Для расчета поля в среде II с диэлектрической постоянной ε ₂ необходимо пользоваться зарядом q ₃ = βq ₁, расположенным на месте заряда q ₁ в среде I с диэлектрической постоянной ε ₁.

Потенциал заряда в МДП‑структуре

Рассмотрим случай, когда точечный заряд находится на границе раздела окисел – полупроводник. Экранировка происходит только затвором структуры (слабая инверсия, низкая плотность поверхностных состояний, стандартное легирование). На рисунке 3.25 изображена возникшая ситуация. Рассмотрим случай, когда нужно сначала рассмотреть поле в окисле структуры. Заряд q, находящийся на границе, отразится зеркально затвором - q, но в этом случае заряд - q – это заряд над границей двух диэлектриков. Из-за поляризации для получения правильного поля в окисле необходимо ввести заряд αq, находящийся по другую сторону на таком же расстоянии от границы раздела. Этот заряд αq в свою очередь снова отразится в затворе и даст заряд - αq. Таким образом, правильное поле в окисле в случае трехслойной МДП‑системы получается только при бесконечном наборе зарядов слева и справа от границы раздела.

Для расчета поля и потенциала в полупроводнике все заряды слева на рисунке 3.25 мы должны уменьшить в β раз согласно предыдущему рассмотрению. Следовательно, величина поля и потенциала в полупроводнике МДП‑структуры обусловлена суммой зарядов + q и противоположного по знаку - βq, + βαq, - βα²q и т.д., отстоящих на расстояние 2 d _ox, 4 d _ox, 6 d _ox, 8 d _ox от границы раздела окисел – полупроводник.

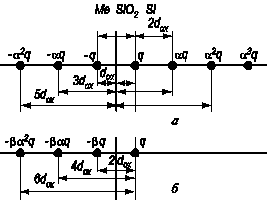
Рис. 3.25. Схема зарядов, необходимая для расчета электрического поля и потенциала МДП‑структуры:

а) в диэлектрике; б) в полупроводнике

Условие электронейтральности соблюдено, заряд слева и справа суммарно равны между собой. Поскольку мы предположили, что заряд находится на границе раздела окисел-полупроводник, то

.

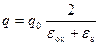Таким образом, потенциал, создаваемый в полупроводнике точечным зарядом, находящимся на границе окисел – полупроводник при экранировке затвором МДП‑структуры, на расстоянии λ вглубь и ρ в плоскости границы раздела можно вписать в виде потенциала распределенного диполя:

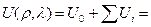
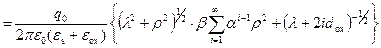. (3.141)

В случае равенства диэлектрических постоянных полупроводника и диэлектрика ε ₁ = ε ₂ = ε ^*, β = 1, α = 0 получаем потенциал простого диполя:

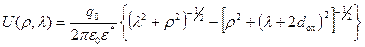. (3.142)

Как следует из соотношений (3.141) и (3.142), различие в потенциалах простого и рассредоточенного диполя будет проявляться при высоких различиях в диэлектрических постоянных окисла и полупроводника, большой толщине диэлектрика d _ox, высоких значениях (по сравнению с толщиной окисла) расстояния вглубь полупроводника λ, где рассчитывается потенциал.

3.7.5. Потенциальный рельеф в МДП‑структуре при дискретности элементарного заряда

Для нахождения вида потенциального рельефа в МДП‑структуре воспользуемся методом математического моделирования. Для этого, используя датчик случайных чисел, на площадке S, соответствующей в случае МДП‑структуры границе раздела полупроводник – диэлектрик, разбрасываются N единичных точечных зарядов со средней плотностью 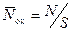. Потенциал каждого заряда рассчитывается с учетом экранировки затвором МДП‑структуры по уравнению (3.141). Как и прежде, предполагается, что реализовано условие слабой инверсии или обеднения и толщина подзатворного диэлектрика d _ox меньше ширины ОПЗ.

Для нахождения вида потенциального рельефа потенциалы всех зарядов суммировались и из полученного значения вычиталось среднее значение величины поверхностного потенциала 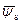, соответствующее квазинепрерывному и равномерному распределению встроенного заряда со средней плотностью .

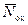На рисунке 3.26 приведена полученная таким образом картина потенциального рельефа. Из рисунка видно, что потенциальный рельеф негладкий, на нем имеются «озера» – участки со значительно меньшим уровнем поверхностного потенциала, «горные хребты» – участки со значительно большим уровнем поверхностного потенциала и, наконец, «долины» – области, где поверхностный потенциал близок к среднему. На приведенной шкале пространственного масштаба видно, что характерный размер областей «озер» и «горных хребтов» составляет порядка 500 Å при толщине диэлектрика d _ox в МДП‑структуре d _ox = 50 Å.

Рис. 3.26. Форма потенциального рельефа в МДП‑структуре в области слабой инверсии. Сплошные линии соответствуют отклонению потенциала ψ _s от среднего значения 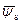на величину среднеквадратичной флуктуации σ _ψ. Точки соответствуют местам расположения зарядов

На рисунке 3.27 приведена зависимость поверхностного потенциала ψ _s от координаты y вдоль границы раздела полупроводник – диэлектрик, рассчитанная для случая, приведенного на рисунке 3.26. Из данного рисунка также видно, что зависимость потенциала ψ _s от координаты является немонотонной функцией.

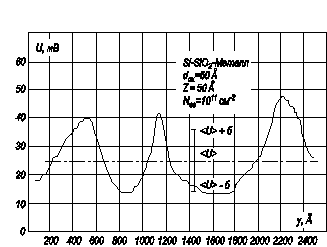
Рис. 3.27. Зависимость потенциала ψ _s от координаты y вдоль поверхности

Таким образом, дискретность и случайный характер расположения в плоскости границы раздела полупроводник – диэлектрик встроенного заряда вызывают флуктуации относительного среднего значения величины поверхностного потенциала.

Date: 2015-05-05; view: 520; Нарушение авторских прав