Зависимость величины среднеквадратичной флуктуации от параметров МДП-структуры

Как следует из разделов 3.7.3 и 3.7.4, для случая слабой инверсии можно получить зависимость величины среднеквадратичной флуктуации от параметров МДП‑структуры. Подставим значение для потенциала единичного заряда U (ρ, λ) в виде (3.142) в выражение (3.136) для величины среднеквадратичной флуктуации потенциала σ _ψ. Для случая ε ₁ = ε ₂ = ε ^* интеграл (3.142) с выражением U (ρ, λ) в виде (3.136) берется в явном виде и получаем:

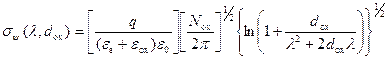. (3.146)

Когда диэлектрические постоянные окисла и полупроводника ε _ox и ε _s сильно отличаются друг от друга, зависимость σ _ψ(λ, d _ox) в аналитическом виде не выражается.

На рисунке 3.31 приведены расчетные зависимости величины среднеквадратичной флуктуации потенциала σ _ψ(λ) при различных толщинах подзатворного диэлектрика. Обращает на себя внимание тот факт, что в случае статистических флуктуаций величина среднеквадратичного отклонения σ _ψ довольно значительно зависит от расстояния λ вглубь полупроводника. По мере уменьшения толщины подзатворного диэлектрика зависимость σ _ψ(λ) увеличивается. Видно также, что чем тоньше подзатворный диэлектрик, тем сильнее экранируются флуктуации и тем меньше величина среднеквадратичной флуктуации потенциала.

Рис. 3.31. Зависимость величины среднеквадратичной флуктуации σ _ψ от расстояния λ вглубь полупроводника, рассчитанная при различных величинах толщины диэлектрика d _ox

Из соотношения (3.146) следует, что по мере приближения к границе раздела при λ → 0 величина среднеквадратичной флуктуации σ _ψ логарифмически стремится к бесконечности. Этот факт обусловлен тем, что потенциал точечного заряда при r → 0 стремится к бесконечности. Как уже отмечалось в предыдущем разделе, функция распределения потенциала P (ψ _s) в этом случае имеет длинный «хвост» в сторону вероятности нахождения больших значений потенциала. Очевидно, что бесконечных значений потенциала на границе раздела не существует. Физическим ограничением на расстояние λ, на которое носители могут приблизиться к заряженному центру, является его конечный размер. Различные оценки приводят к величине ρ _min = (5÷100) Å в интеграле (3.136) и соответствующей замене нижнего предела интегрирования с нуля на величину ρ _min.

При расчете среднеквадратичной флуктуации σ _ψ(λ, d _ox) с использованием значения потенциала U (ρ, λ) в виде распределенного диполя по уравнению (3.141) и дальнейшего численного расчета интеграла σ _ψ(λ, d _ox) по уравнению (3.136) получено незначительное расхождение между значениями среднеквадратичной флуктуации по сравнению с сосредоточенным диполем только в области малых значений λ. Это позволяет в дальнейшем использовать для расчетов зависимости σ _ψ(λ, d _ox) явное выражение в виде (3.152).

Рассмотрев зависимость величины среднеквадратичной флуктуации σ _ψ от параметров МДП‑структуры применительно к переносу заряда в инверсионном канале, Брюс получил аналогичную зависимость в виде:

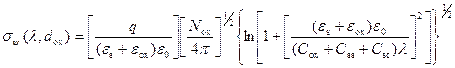, (3.147)

где C _ox, C _ss, C _sc – удельная емкость окисла, поверхностных состояний и полупроводника,

λ – среднее расстояние носителей в инверсионном слое до поверхности.

Выражение (3.147) для σ _ψ было получено Брюсом из решения уравнения Пуассона с использованием функций Грина. Для областей слабой инверсии выражение (3.147) принимает вид:

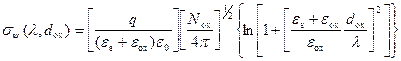. (3.148)

Для случая λ >> d _ox выражения (3.148) и (3.146) дают одинаковое функциональное поведение зависимости σ _ψ ~ λ ^-1 и отличаются по величине в 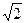раз. В области малых величин λ ~ d _ox зависимости σ _ψ(λ) также несколько отличаются.

Date: 2015-05-05; view: 489; Нарушение авторских прав