Функция распределения потенциала при статистических флуктуациях

При рассмотрении флуктуаций поверхностного потенциала вопрос о нахождении вида функций распределения является одним из важных. Поскольку заряженные центры в МДП‑структуре дискретны и случайным образом распределены в плоскости границы раздела, то их закон распределения описывается уравнением Пуассона:

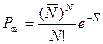, (3.143)

где N – число зарядов, ожидаемое найти на площадке S,

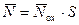– среднее число зарядов, находящееся на произвольной площадке S.

Координаты каждого заряда в плоскости ρ _i являются случайной функцией, а общий потенциал от всех зарядов в произвольной точке ОПЗ полупроводника на расстоянии λ будет суммой потенциалов всех точечных зарядов в виде (3.141):

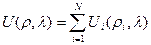. (3.144)

В явном виде совместное решение уравнений (3.141 – 3.144) возможно только при условии λ >> d _ox, .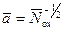

В этом случае закон распределения потенциала ψ _s описывается гауссовым распределением:

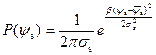, (3.145)

где σ _s – относительная среднеквадратичная флуктуация потенциала ψ _s на расстоянии λ. Поскольку в общем виде соотношения (3.141 – 3.144) не представляется возможным решать в аналитическом виде, для нахождения функции распределения P (ψ _s) использовалось численное моделирование, аналогичное описанному в разделе 3.7.5. Генерируя n раз датчиком случайных чисел координаты всех зарядов, рассчитывалось в произвольной, заранее выбранной точке значение суммарного потенциала. Частота выпадания того или иного значения потенциала соответствовала плотности вероятности.

На рисунке 3.28 показан вид функции распределения поверхностного потенциала ψ _s для МДП‑структур с различной толщиной подзатворного диэлектрика в диапазоне d _ox = (50÷1000) Å. Заметим, что функции не нормированы.

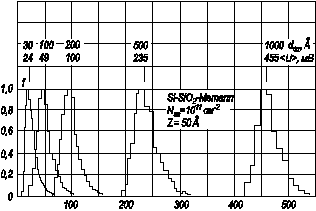
Рис. 3.28. Вид функции распределения f потенциала в МДП‑структурах с разной толщиной диэлектрика

Из рисунка видно, что при малых значениях толщины окисла d _ox функция распределения отличается от гауссовой. По мере роста толщины диэлектрика распределение потенциала приближается к нормальному.

На рисунке 3.29 показана зависимость функции распределения от средней плотности заряда на границе раздела окисел – полупроводник.

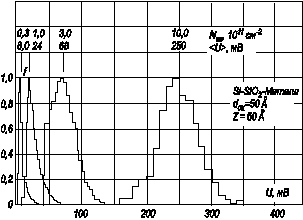
Рис. 3.29. Вид функции распределения f потенциала в МДП‑структуре при разной величине плотности заряда

Также видно, что при малых плотностях 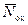функция распределения отличается от гауссовой, по мере роста числа зарядов 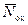распределение потенциала также приближается к линейному.

На рисунке 3.30 показано изменение вида функции распределения по мере приближения к границе раздела окисел – полупроводник. Видно, что средняя часть функции распределения не меняется, но «хвост» функции в сторону вероятности получения больших значений потенциала, по мере приближения к границе раздела, возрастает.

Физическая картина, обуславливающая отличие вида функции распределения поверхностного потенциала ψ _s от нормального распределения, заключается в том, что потенциал кулоновского точечного центра резко зависит от расстояния r при малых значениях r.

Рис. 3.30. Вид функции распределения f потенциала в МДП‑структуре при различных расстояниях λ вглубь полупроводника

Date: 2015-05-05; view: 481; Нарушение авторских прав