Конденсаторная модель Гоетцбергера для флуктуаций поверхностного потенциала

Пусть флуктуации поверхностного потенциала обусловлены крупномасштабными технологическими флуктуациями плотности встроенного в диэлектрик заряда Q _ox = qN _ox. Толщина подзатворного диэлектрика d _ox и концентрация легирующей примеси N _D,A, как видно из рисунка 3.22а, б, остается постоянной.

Рассмотрим, каким образом можно получить функции распределения P (ψ _s) поверхностного потенциала ψ _s вдоль границы раздела полупроводник – диэлектрик. Пусть 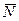– среднее число заряженных центров на границе раздела полупроводник – диэлектрик, приходящееся на характеристическую площадку α _s. Под характеристической площадкой α _s будем понимать ту минимальную площадь, на которую можно разбить МДП‑структуру, чтобы в пределах этой площадки величина поверхностного потенциала была одинакова. Если 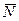– большое число, то функция P (N) будет гауссовской аппроксимацией распределения Пуассона:

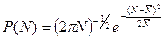. (3.122)

Величина N и плотность заряда Q _ox на площадке α _s связаны очевидным соотношением:

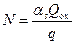. (3.123)

Комбинируя (3.122) и (3.123), получаем для функции распределения плотности заряда P (Q _ox):

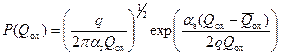. (3.124)

Для функции распределения поверхностного потенциала имеем:

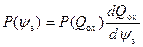. (3.125)

Продифференцировав уравнение электронейтральности в виде (3.121) и учитывая, что 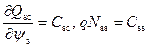, а также, что величина dV _G = 0, так как напряжение V _G одинаково для каждой характеристической площадки α _s, получаем:

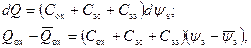(3.126)

где 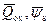– среднее значение заряда Q _ox и поверхностного потенциала ψ _s.

Подставляя в уравнение (3.125) для функции распределения P (ψ _s) соотношения (3.126) и (3.124), имеем:

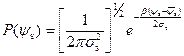, (3.127)

где величина относительной среднеквадратичной флуктуации потенциала 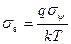равняется:

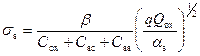. (3.128)

Среднеквадратичная флуктуация потенциала σ _ψ, определяющая отклонение ψ _s от среднего значения 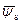, будет равна:

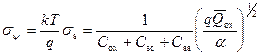. (3.129)

Из соотношения (3.128) следует, что флуктуации потенциала описываются в конденсаторной модели нормальным распределением. Величина среднеквадратичной флуктуации потенциала определяется толщиной диэлектрика d _ox, плотностью поверхностных состояний N _ss, величиной средней плотности заряженных центров 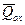на границе раздела. Величина α _s, входящая в (3.128), в рассмотрении точно не определена. Сравнение теоретического рассмотрения конденсаторной модели с экспериментом по анализу кривых нормированной проводимости G _p/ ω показало, что величина площадки α _s равна в области обеднения МДП‑структуры квадрату ширины обедненной области (рис. 3.23).

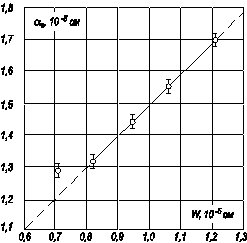
Рис. 3.23. Зависимость площадки α _s от ширины области обеднения W

Date: 2015-05-05; view: 466; Нарушение авторских прав