Среднеквадратичная флуктуация потенциала, обусловленная системой случайных точечных зарядов

Рассмотрим систему зарядов на бесконечной плоскости, координата каждого из которых является случайной функцией. Заряды будем считать малыми и находящимися в узлах со средним расстоянием между узлами 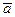. Плотность узлов 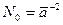значительно больше, чем средняя плотность зарядов 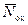. Вероятность заполнения одного узла α << 1 и равна .

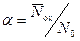Потенциал, который создает произвольный узел в некоторой точке A на расстоянии 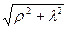от него, будет равен:

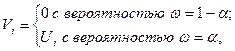(3.130)

где U _i – потенциал, создаваемый заряженным узлом в точке A,

ρ – расстояние в плоскости от начала координат до заряда,

λ – расстояние от точки A, где ищется потенциал, до плоскости, где расположены заряды.

Средняя величина потенциала 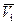, создаваемого i -м узлом, по определению среднего,

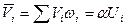. (3.131)

Для расчета среднеквадратичного отклонения запишем:

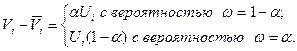
Тогда среднеквадратичное отклонение величины V _i будет равно:

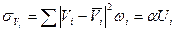, (3.132)

учитывая, что α << 1.

Потенциал U, создаваемый всей совокупностью зарядов на плоскости в точке A с координатами (ρ, λ), будет равен:

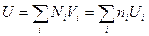, (3.133)

где N _i – число узлов на расстоянии r _i,

n _i – число заполненных узлов на расстоянии r _i.

Учитывая, что заполнение и расположение узлов является случайным, для величины среднеквадратичного отклонения потенциала в точке A с координатами (ρ, λ), обусловленного всеми зарядами, получаем, учитывая (3.133),

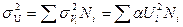. (3.134)

Рассмотрим количество узлов N _i в интервале (ρ, ρ+αρ) около точки A. Оно будет:

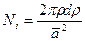. (3.135)

Учитывая определение вероятности заполнения узла α и (3.134), из (3.135) получаем:

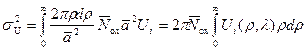. (3.136)

В полученном выражении величина U _i(ρ, λ) имеет смысл потенциала единичного точечного заряда. Таким образом, из (3.136) можно видеть, что величина среднеквадратичной флуктуации потенциала σ _U, вызванной системой точечных зарядов, определяется только их плотностью и потенциалом одного такого заряда.

Date: 2015-05-05; view: 521; Нарушение авторских прав