Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пересекающиеся плоскости
Третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой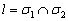 
:
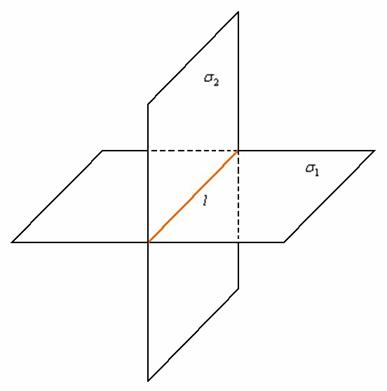
Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных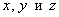
НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства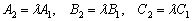 
Сразу отмечу важный факт: Если плоскости пересекаются, тосистема линейных уравнений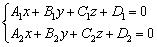
задаёт уравнение прямой в пространстве. Но о пространственной прямой позже.
В качестве примера рассмотрим плоскости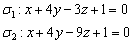 
. Составим систему для соответствующих коэффициентов:
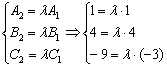
Из первых двух уравнений следует, что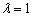 
, но из третьего уравнения следует, что 
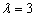, значит, система несовместна, и плоскости пересекаются.
Проверку можно выполнить «по пижонски» одной строкой:
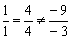
Параллельные плоскости мы уже разобрали, теперь поговорим о перпендикулярных плоскостях. Очевидно, что к любой плоскости можно провести бесконечно много перпендикулярных плоскостей, а для того, чтобы зафиксировать конкретную перпендикулярную плоскость, необходимо знать две точки:
Пример 12
Дана плоскость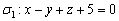 
. Построить плоскость 
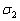, перпендикулярную данной и проходящую через точки 
.
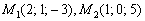Решение: Начинаем анализировать условие. Что мы знаем о плоскости 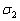? Известны две точки. Можно найти вектор 
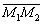, параллельный данной плоскости. Маловато. Было бы неплохо где-нибудь нарыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор плоскости 
.
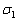Проводить подобные рассуждения здОрово помогает схематический чертёж:
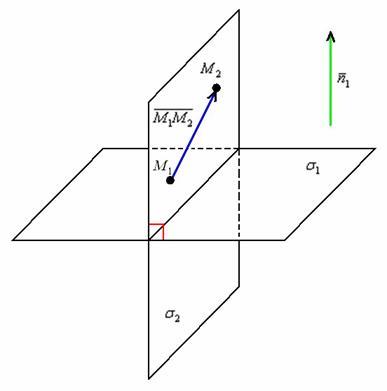
Для лучшего понимания задачи отложите вектор нормали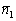 
от точки 
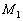в плоскости .
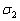Следует заметить, что две произвольные точки могут располагаться в пространстве как угодно, и перпендикулярная плоскость может быть развёрнута к нам совершенно другим ракурсом. Кстати, теперь чётко видно, почему одна точка не определит перпендикулярную плоскость – вокруг единственной точки будет «вращаться» бесконечно много перпендикулярных плоскостей. Так же нас не устроит и единственный вектор (без всяких точек). Вектор является свободным и «наштампует» нам бесконечно много перпендикулярных плоскостей (которые, к слову, все будут параллельны). В этой связи минимальную жёсткую конструкцию обеспечивают две точки.
Алгоритм разобран, решаем задачу:
1) Найдём вектор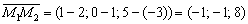 
.
2) Из уравнения 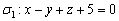снимем вектор нормали: 
.
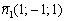3) Уравнение плоскости 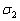составим по точке 
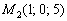(можно было взять и 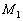) и двум неколлинеарным векторам 
:
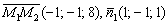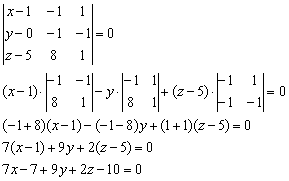
Ответ: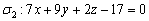 
Проверка состоит из двух этапов:
1) Проверяем, действительно ли плоскости будут перпендикулярны. Если две плоскости перпендикулярны, то их векторы нормали будут ортогональны. Логично. Из полученного уравнения 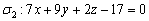снимаем вектор нормали 
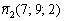и рассчитываем скалярное произведение векторов:
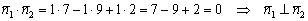
Таким образом,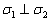 
2) В уравнение плоскости 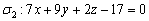подставляем координаты точек 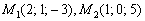. Обе точки должны «подойти».
И первый, и второй пункт можно выполнить устно.
Перейдём к заключительной задаче урока:
Date: 2015-04-23; view: 1567; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |