Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Взаимное расположение трёх плоскостей
|
|
Три плоскости могут располагаться в пространстве 8-ю способами, если интересуют все случаи, пожалуйста, посмотрите в книге Атанасяна-Базылева или в Интернете, видел вроде в Википедии, точно уже не помню.
Самый известный случай взаимного расположения трёх плоскостей – плоскости пересекаются в одной точке. Живой пример находится совсем недалеко от вас. Посмотрите вверх – в угол комнаты, где пересекаются две стены и потолок. Пессимисты могут посмотреть вниз.
Аналитически данному случаю соответствует система линейных уравнений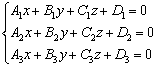 
, которая имеет единственное решение.
Ничего не напоминает? Вот, оказывается, где прячется метод Крамера … – в углу вашей комнаты!
На следующем уроке мы изучим Прямые в пространстве.
Спасибо за работу, домашнего задания не будет!
Решения и ответы:
Пример 2: Решение: составим уравнение плоскости по точке и двум неколлинеарным векторам:
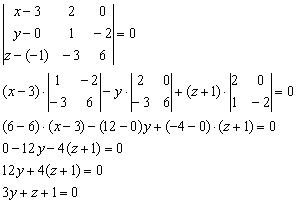
Ответ: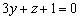 
Пример 4: Решение: составим уравнение плоскости по трём точкам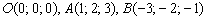 
:
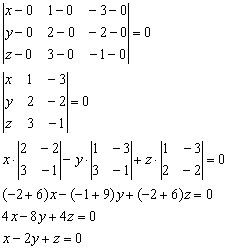
Ответ: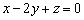 
Пример 7: Решение: Так как плоскость перпендикулярна оси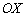 
, то вектор 
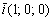является вектором нормали для данной плоскости. Уравнение плоскости составим по точке 
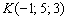и вектору нормали :
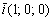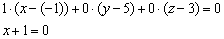
Ответ: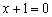 
Пример 11: Решение: Разделим все коэффициенты второго уравнения на два:
Используем формулу
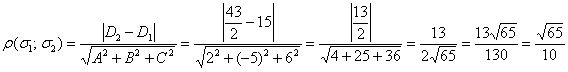
Ответ: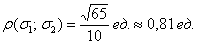 
Пример 13: Решение: Обозначим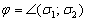 
. Используем формулу:
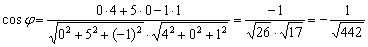
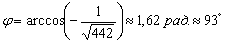
За угол между плоскостями примем острый угол: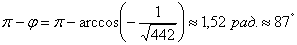 
Ответ: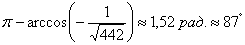 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
УравнениЯ прямой в пространстве
Здравствуйте-здравствуйте! Впервые или снова, но очень рад вас видеть! Продолжаем знакомиться с пространственной геометрией – миром, в котором мы живём. На первом уроке мы вдоль и поперёк рассмотрели уравнение плоскости, а сейчас очередь дошла до моей очередной жертвы – прямой в пространстве. Если ваш уровень подготовки не очень высок, пожалуйста, начните с предыдущей статьи, там же есть путеводитель для чайников – тех, кто проходил мимо векторов пару раз и очень давно.
В данном разделе мы разберём вопросы, связанные с уравнениЯМИ прямой в пространстве, посмотрим, как может располагаться прямая относительно координатных плоскостей, координатных осей и научимся решать типовые задачи. Я добросовестно постараюсь рассказать всё самое главное, что связано с пространственными прямыми.
Начнём с уравненИЙ прямой в пространстве. Для лёгкого понимания темы целесообразно хорошо проштудировать уравнение «плоской» прямой, поскольку будет очень много похожих вещей. Но будут и отличия, на одно из которых вы уже наверняка обратили внимание. Я выделял большими буквами окончание слова «уравнение», подчеркивая, что оно находится ВО МНОЖЕСТВЕННОМ ЧИСЛЕ. И это не случайно, своеобразие пространственной прямой состоит в том, что она задаётся не одним уравнением, а некоторым множеством уравнений. Высшая математика не озадачивает нас улыбкой Джоконды, поэтому надвинем на лоб строгую параллельность морщин и приступим к делу:
Date: 2015-04-23; view: 1771; Нарушение авторских прав