Типовая задача с треугольником на плоскости

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в сердцАх сказал один мой одноклассник, «не понимаю, на… доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не будем ничего доказывать, поскольку аналитическая геометрия подкрадывается к треугольнику совсем с другой стороны.

Типовая задача с треугольником на плоскости, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше.

Пример 1

Даны вершины треугольника 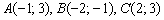. Требуется:

1) составить уравнения сторон 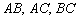и найти их угловые коэффициенты;
2) найти длину стороны ;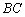
3) найти ;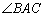
4) составить уравнение прямой 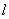, проходящей через точку 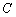параллельно прямой ;
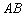5) составить уравнение высоты 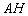и найти её длину;
6) вычислить площадь треугольника ;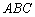
7) составить уравнение медианы ;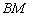
8) найти точку пересечения .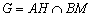

Знаете, прямо почувствовал себя палачом с большим топором. Чтобы не было так стыдно, скажу, что на практике в большинстве случаев пунктов бывает меньше. Просто я постарался собрать в одной задаче всё, что может встретиться. Для особо опасных энтузиастов заготовлена виселица ещё тройка пунктов, но это на закуску.

…бррр, что-то у меня сегодня траурная тема пошла, не иначе, от убыли светового дня. Поэтому скорее перехожу к решению.

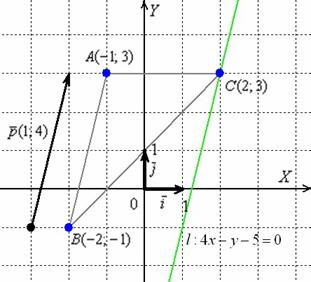
Решение: С чего начать? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и самопроверки всегда строим чертёж на черновике.

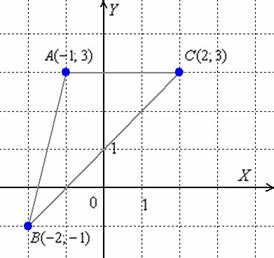
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1 см (2 тетрадные клетки).

Поехали щёлкать орехи:

1) Составим уравнения сторон 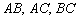и найдём их угловые коэффициенты.

Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум точкам. Процесс подробно рассмотрен на уроке Уравнение прямой на плоскости.

Составим уравнение стороны 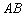по точкам :

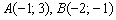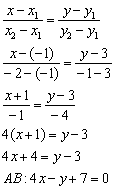
Для проверки следует мысленно либо на черновике подставить координаты каждой точки в полученное уравнение. Теперь найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

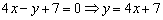
Таким образом, угловой коэффициент: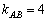

Аналогично находим уравнения сторон 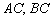. Не вижу особого смысла расписывать то же самое, поэтому сразу приведу готовый результат:

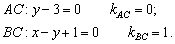
2) Найдём длину стороны 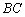. Это простейшая задача, рассмотренная на уроке Векторы для чайников. Для точек 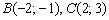используем формулу:

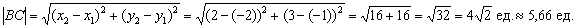
По этой же формуле легко найти и длины других сторон. Проверка очень быстро выполнятся обычной линейкой.

3) Найдём 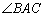. Это угол при вершине 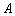. Есть несколько способов решения, но самый универсальный способ – находить угол при вершине, как угол между векторами. Данная задача подробно рассмотрена на уроке Скалярное произведение векторов.

Используем формулу .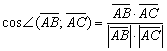

Найдём векторы:

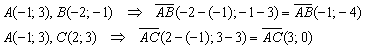
Таким образом:

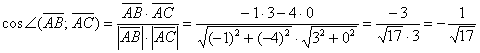
Кстати, попутно мы нашли длины сторон .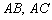

В результате:

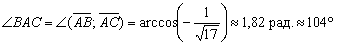
Ну что же, похоже на правду, для убедительности к углу можно приложить транспортир.

Внимание! Не путайте угол треугольника с углом между прямыми. Угол треугольника может быть тупым, а угол между прямыми – нет (см. последний параграф статьи Простейшие задачи с прямой на плоскости). Однако для нахождения угла треугольника можно использовать и формулы вышеуказанного урока, но шероховатость состоит в том, что те формулы всегда дают острый угол. С их помощью я прорешал на черновике данную задачу и получил результат 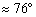. А на чистовике пришлось бы записывать дополнительные оправдания, что .

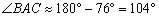4) Составить уравнение прямой 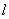, проходящей через точку 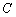параллельно прямой .

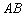Стандартная задача, подробно рассмотренная в примере №2 урока Простейшие задачи с прямой на плоскости. Из общего уравнения прямой 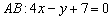вытащим направляющий вектор 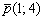. Составим уравнение прямой 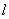по точке 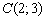и направляющему вектору :

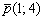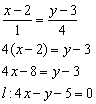
Date: 2015-04-23; view: 1088; Нарушение авторских прав