Линейные неравенства

Различают два типа линейных неравенств:

1) Строгие неравенства: .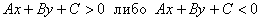

2) Нестрогие неравенства: .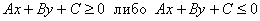

Какой геометрический смысл этих неравенств? Если линейное уравнение 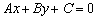задаёт прямую, то линейное неравенство определяет полуплоскость.

Для понимания нижеследующей информации нужно знать разновидности прямых на плоскости и уметь строить прямые. Если возникнут трудности в этой части, прочитайте справку Графики и свойства функций – параграф про линейную функцию.

Начнём с простейших линейных неравенств. Голубая мечта любого двоечника – координатная плоскость, на которой нет ничегошеньки:

Как известно, ось абсцисс 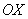задаётся уравнением 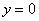– «игрек» всегда (при любом значении «икс») равняется нулю

Рассмотрим неравенство 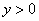. Как его понимать неформально? «Игрек» всегда (при любом значении «икс») положителен. Очевидно, что данное неравенство определяет верхнюю полуплоскость – ведь там и находятся все точки с положительными «игреками».

В том случае, если неравенство нестрогое 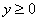, к верхней полуплоскости дополнительно добавляется сама ось .

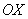Аналогично: неравенству 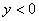удовлетворяют все точки нижней полуплоскости, нестрогому неравенству 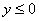соответствует нижняя полуплоскость + ось .

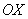С осью ординат 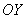та же самая прозаичная история:

– неравенство 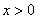задаёт правую полуплоскость;
– неравенство 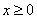задаёт правую полуплоскость, включая ось ординат;
– неравенство 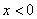задаёт левую полуплоскость;
– неравенство 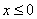задаёт левую полуплоскость, включая ось ординат.

На втором шаге рассмотрим неравенства, в которых отсутствует одна из переменных.

Отсутствует «игрек»:

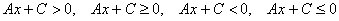
Или отсутствует «икс»:

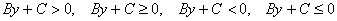
С такими неравенствами можно разобраться двумя способами, пожалуйста, рассмотрите оба подхода. Попутно вспомним-закрепим школьные действия с неравенствами, уже разобранные на уроке Область определения функции.

Пример 1

Решить линейные неравенства:

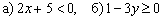
Date: 2015-04-23; view: 779; Нарушение авторских прав