Как найти центр тяжести треугольника?

10) А что такое вообще центр тяжести плоской фигуры? Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке. Из пункта №7 нам уже известна одна из медиан: 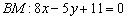. Как решить задачу? Можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь короче! Нужно только знать полезное свойство:

Точка пересечения медиан делит каждую из медиан в отношении , считая от вершины треугольника. Поэтому справедливо отношение

Нам известны точки .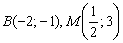
По формулам деления отрезка в данном отношении:

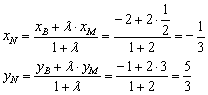
Таким образом, центр тяжести треугольника: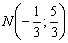

Заключительный пункт урока:

11) Составим систему линейных неравенств, определяющих треугольник.

Для понимания решения необходимо хорошо изучить статью Линейные неравенства. Системы линейных неравенств.

Для удобства перепишем найденные уравнения сторон:

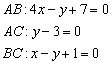
Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится вершина 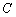. Составим вспомогательный многочлен 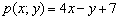и вычислим его значение в точке 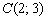: 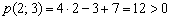. Поскольку сторона 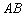принадлежит треугольнику, то неравенство будет нестрогим:

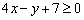
Если не понятно, что к чему, пожалуйста, вернитесь к материалам про линейные неравенства.

Рассмотрим прямую 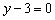. Треугольник расположен ниже данной прямой, поэтому очевидно неравенство .

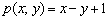И, наконец, для прямой составим многочлен , в который подставим координаты точки 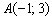: 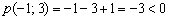. Таким образом, получаем третье неравенство: .

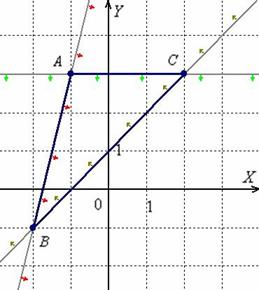
Итак, треугольник 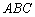определяется следующей системой линейных неравенств:

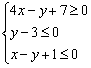
Приехали.

Как уже отмечалось, на практике рассмотренная задача с треугольником на плоскости очень популярна. Пунктов решения будет, конечно, не одиннадцать, а меньше, причём встретиться они могут в самых различных комбинациях. В этой связи вам придётся самостоятельно протягивать логическую цепочку решения. А вообще, всё довольно однообразно.

Может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =) Ненасытные читатели могут ознакомиться с решениями других задач по аналитической геометрии. Подходящий архив можно закачать на странице Готовые задачи по высшей математике.

Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них! Главное, придерживаться методики решения, которая освещена в самом начале урока. А теперь можно немного расслабиться, заданий для самостоятельного решения я не придумал. Кандидатур было много, но по основным приёмам решения все они до неприличия похожи на разобранные примеры.

Приятных треугольных сновидений!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Линии второго порядка.
Эллипс и его каноническое уравнение. Окружность

После основательной проработки прямых на плоскости продолжаем изучать геометрию двухмерного мира. Ставки удваиваются, и я приглашаю вас посетить живописную галерею эллипсов, гипербол, парабол, которые являются типичными представителями линий второго порядка. Экскурсия уже началась, и сначала краткая информация обо всей экспозиции на разных этажах музея:

Date: 2015-04-23; view: 1435; Нарушение авторских прав