Что значит решить систему линейных неравенств?

Решить систему линейных неравенств – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы.

В качестве простейших примеров рассмотрим системы неравенств, определяющих координатные четверти прямоугольной системы координат («рисунок двоечников» находится в самом начале урока):

Система неравенств 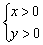задаёт первую координатную четверть (правая верхняя). Координаты любой точки первой четверти, например, 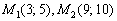и т.д. удовлетворяют каждому неравенству данной системы.

Аналогично:
– система неравенств 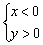задаёт вторую координатную четверть (левая верхняя);
– система неравенств 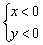задаёт третью координатную четверть (левая нижняя);
– система неравенств 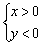задаёт четвёртую координатную четверть (правая нижняя).

Система линейных неравенств может не иметь решений, то есть, быть несовместной. Снова простейший пример: 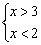. Совершенно очевидно, что «икс» не может одновременно быть больше трёх и меньше двух.

Решением системы неравенств может являться прямая, например: 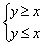. Лебедь, рак, без щуки, тянут воз в две разные стороны. Да воз и ныне там – решением данной системы является прямая .

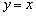Но самый распространённый случай, когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называется многоугольником решений системы.

Пример 7

Решить систему линейных неравенств

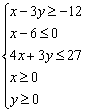
На практике в большинстве случаев приходится иметь дело с нестрогими неравенствами, поэтому оставшуюся часть урока водить хороводы будут именно они.

Решение: то, что неравенств многовато, пугать не должно. Сколько может быть неравенств в системе? Да сколько угодно. Главное, придерживаться рационального алгоритма построения области решений:

1) Сначала разбираемся с простейшими неравенствами. Неравенства определяют первую координатную четверть, включая границу из координатных осей. Уже значительно легче, так как область поиска значительно сузилась. На чертеже сразу отмечаем стрелочками соответствующие полуплоскости (красные и синие стрелки)

2) Второе по простоте неравенство – здесь отсутствует «игрек». Во-первых, строим саму прямую 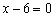, а, во-вторых, после преобразования неравенства к виду , сразу становится понятно, что все «иксы» меньше, чем 6. Отмечаем зелёными стрелками соответствующую полуплоскость. Ну что же, область поиска стала ещё меньше – такой не ограниченный сверху прямоугольник.

3) На последнем шаге решаем неравенства «с полной амуницией»: 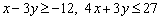. Алгоритм решения мы подробно рассмотрели в предыдущем параграфе. Вкратце: сначала строим прямую, потом с помощью подопытной точки находим нужную нам полуплоскость.

Встаньте, дети, встаньте в круг:

Область решений системы представляет собой многоугольник 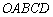, на чертеже он обведён малиновой линией и заштрихован. Перестарался немного =) В тетради область решений достаточно либо заштриховать, либо жирнее обвести простым карандашом.

Любая точка данного многоугольника удовлетворяет КАЖДОМУ неравенству системы (для интереса можете проверить).

Ответ: решением системы является многоугольник .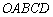

При оформлении на чистовик неплохо бы подробно расписать, по каким точкам вы строили прямые (см. урок Графики и свойства функций), и как определяли полуплоскости (см. первый параграф данного урока). Однако на практике в большинстве случаев вам зачтут и просто правильный чертёж. Сами же расчёты можно проводить на черновике или даже устно.

Помимо многоугольника решений системы, на практике, пусть и реже, встречается открытая область. Попытайтесь разобрать следующий пример самостоятельно. Хотя, точности ради, пыток тут никаких – алгоритм построения такой же, просто область получится не ограниченной.

Пример 8

Решить систему

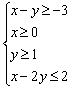
Решение и ответ в конце урока. У вас, скорее всего, будут другие буквенные обозначения вершин полученной области. Это не принципиально, главное, правильно найти вершины и правильно построить область.

Не редкость, когда в задачах требуется не только построить область решений системы, но и найти координаты вершин области. В двух предыдущих примерах координаты данных точек были очевидны, но на практике всё бывает далеко не айс:

Пример 9

Решить систему и найти координаты вершин полученной области

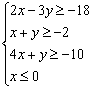
Решение: изобразим на чертеже область решений данной системы. Неравенство 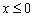задаёт левую полуплоскость с осью ординат, и халявы тут больше нет. После расчётов на чистовике/черновике или глубоких мыслительных процессов, получаем следующую область решений:

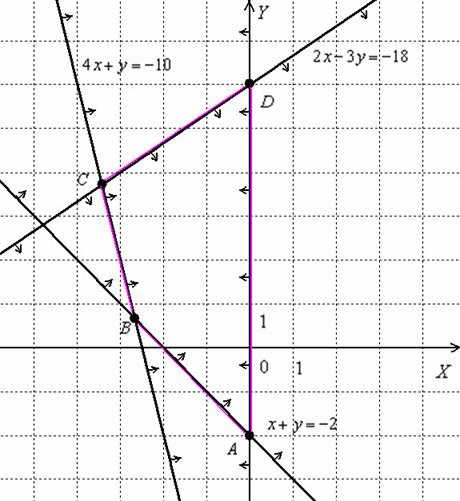
Область решений представляет собой многоугольник 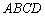. Теперь нужно найти координаты вершин полученной области. Здесь ясно прорисовались координаты только двух точек: . Остаётся решить вопрос с точками .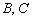

Нетрудно заметить, что вершины 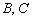являются точками пересечением прямых. Как найти точку пересечения двух прямых, мы рассмотрели на уроке Задачи с прямой на плоскости.

Найдём координаты вершины :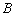

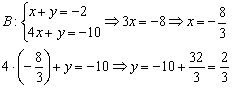
Примечание: из второго уравнения системы почленно вычтено первое уравнение. Более подробно о методе можно прочитать в статье Как решить систему уравнений?

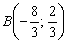
Найдём координаты точки :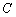

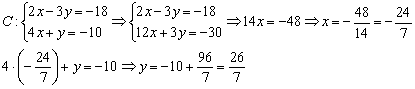
Примечание: второе уравнение системы умножено на 3, затем уравнения сложены почленно.

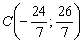
Для красоты координаты точек 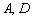тоже можно найти аналитическим методом:

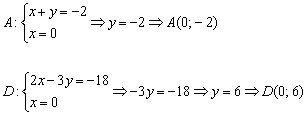
Ответ: область решений системы представляет собой многоугольник с вершинами в точках .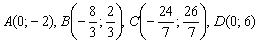

Кто из вас попадёт в «десятку»? Заключительный пример урока для самостоятельного решения:

Пример 10

Найти область решений системы и координаты вершин полученной области

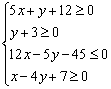
И опять же, буквенные обозначения вершин многоугольника у нас могут отличаться. У меня будет точка «цэ», а у вас эта же вершина может быть обозначена через «дэ».

Мы рассмотрели примеры средней степени сложности, чего вполне достаточно. В ряде задач, например, в задаче линейного программирования коэффициенты неравенств обычно велики, и приходиться возиться (иногда долго) с подбором масштаба и построением самих прямых.

Желаю успехов!

Решения и ответы:

Пример 2: Ответ:

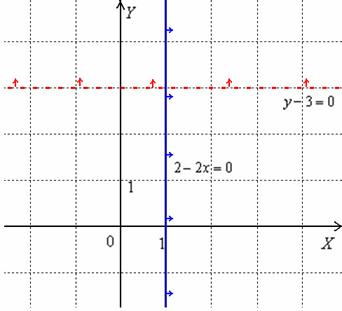
Пример 4: Решение:
а) Построим прямую 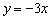. Выберем произвольную точку плоскости, не принадлежащую данной прямой, например, 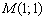и подставим её координаты в неравенство:

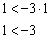
Получено неверное неравенство, значит, неравенство задаёт полуплоскость, которой не принадлежит точка 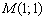, при этом прямая 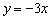не входит в решение.
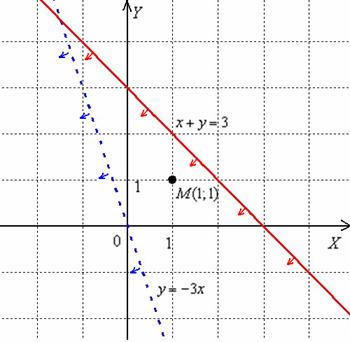
б) Построим прямую 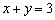. Выберем произвольную точку плоскости, не принадлежащую данной прямой, например, 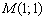и подставим её координаты в неравенство:

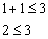
Получено верное неравенство, значит, неравенство 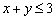задаёт полуплоскость, в которой находится точка 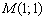, при этом прямая 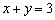входит в решение.
Ответ:

Пример 6: Решение: Составим многочлен 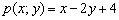и вычислим его значение в точке :
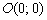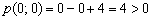, следовательно, искомые точки должны удовлетворять неравенству 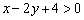(а значит, и условию ).
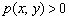Вычислим значения многочлена в каждой из пяти точек:

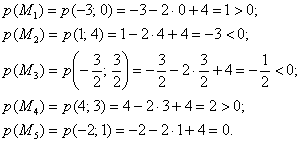
Условию 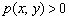удовлетворяют точки .
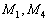Ответ: в одной полуплоскости с началом координат лежат точки .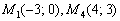

Пример 8: Решение: изобразим на чертеже область решений, соответствующую заданной системе линейных неравенств:

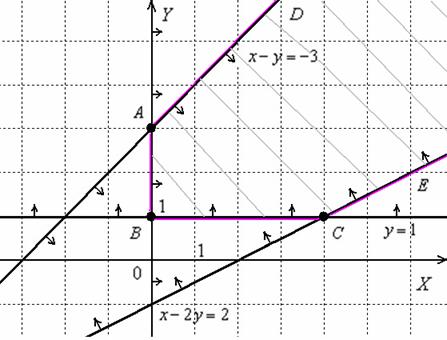
Ответ: область решений системы ограничена ломаной 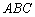и лучами .

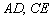Пример 10: Решение: изобразим на чертеже область решений данной системы неравенств:

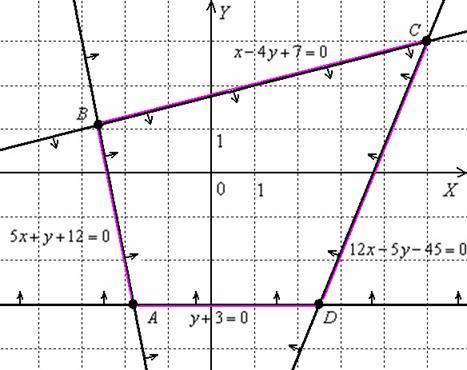
Область решений представляет собой многоугольник 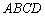. Найдём координаты вершин полученной области:

Ответ: область решений системы представляет собой многоугольник с вершинами в точках .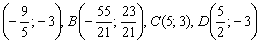

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Как научиться решать задачи по аналитической геометрии?
Типовая задача с треугольником на плоскости

Этот урок создан на подходе к экватору между геометрией плоскости и геометрией пространства. В данный момент назрела необходимость систематизировать наработанную информацию и ответить на очень важный вопрос: как научиться решать задачи по аналитической геометрии? Трудность состоит в том, что задач по геометрии можно придумать бесконечно много, и никакой учебник не вместит в себя всё множество и разнообразие примеров. Это не производная функции с пятью правилами дифференцирования, таблицей и несколькими техническими приёмами….

Решение есть! Не буду говорить громких слов о том, что я разработал какую-то грандиозную методику, однако, по моему мнению, существует эффективный подход к рассматриваемой проблеме, позволяющий достигнуть хорошей и отличной результативности даже полному чайнику. По крайне мере, общий алгоритм решения геометрических задач очень чётко оформился в моей голове.

Date: 2015-04-23; view: 1569; Нарушение авторских прав