ЧТО НЕОБХОДИМО знать и уметь для успешного решения задач по геометрии?

От этого никуда не деться – чтобы наугад не тыкать носом кнопки, требуется освоить азы аналитической геометрии. Поэтому если вы только-только приступили к изучению геометрии или капитально позабыли её, пожалуйста, начните с урока Векторы для чайников. Кроме векторов и действий с ними, нужно знать базовые понятия геометрии плоскости, в частности, уравнение прямой на плоскости и простейшие задачи с прямой на плоскости. Геометрия пространства представлена статьями Уравнение плоскости, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость и некоторыми другими уроками. Кривые линии и пространственные поверхности второго порядка стоЯт некоторым особняком, и специфических задач с ними не так уж много.

Предположим, студент уже обладает элементарными знаниями и навыками решения простейших задач аналитической геометрии. Но вот бывает же так: читаешь условие задачи, и… хочется вообще закрыть всё это дело, закинуть в дальний угол и забыть, как о страшном сне. Причём это принципиально не зависит от уровня вашей квалификации, сам время от времени сталкиваюсь с заданиями, у которых решение не очевидно. Как поступать в таких случаях? Не нужно бояться задачи, которая вам не понятна!

Во-первых, следует установить – это «плоская» или пространственная задача? Например, если в условии фигурируют векторы с двумя координатами, то, понятно, тут геометрия плоскости. А если преподаватель загрузил благодарного слушателя пирамидой, то здесь явно геометрия пространства. Результаты первого шага уже неплохи, ведь удалось отсечь громадное количество ненужной для данной задачи информации!

Второе. Условие, как правило, озаботит вас некоторой геометрической фигурой. Действительно, пройдитесь по коридорам родного ВУЗа, и вы увидите очень много озабоченных лиц.

В «плоских» задачах, не говоря о разумеющихся точках и прямых, наиболее популярная фигура – треугольник. Его гадёныша мы разберём очень подробно. Далее идёт параллелограмм, и значительно реже встречаются прямоугольник, квадрат, ромб, окружность, др. фигуры.

В пространственных задачах могут летать те же плоские фигуры + сами плоскости и распространённые треугольные пирамиды с параллелепипедами.

Вопрос второй – всё ли вы знаете о данной фигуре? Предположим, в условии идёт речь о равнобедренном треугольнике, а вы весьма смутно помните, что это такой за треугольник. Открываем школьный учебник и читаем про равнобедренный треугольник. Что делать… врач сказал ромб, значит, ромб. Аналитическая геометрия аналитической геометрией, но задачу помогут решить геометрические свойства самих фигур, известные нам из школьной программы. Если не знать, чему равна сумма углов треугольника, то мучиться можно долго.

Третье. ВСЕГДА старайтесь выполнять чертёж (на черновике/чистовике/мысленно), даже если этого не требуется по условию. В «плоских» задачах сам Евклид велел взять в руки линейку с карандашом – и не только для того, чтобы понять условие, но и в целях самопроверки. При этом наиболее удобный масштаб 1 единица = 1 см (2 тетрадные клетки). Уж не будем рассуждать о нерадивых студентах и вращающихся в гробах математиках – в таких задачах совершить ошибку практически невозможно. Для пространственных заданий выполняем схематический рисунок, который тоже поможет проанализировать условие.

Чертёж или схематический чертёж зачастую сразу позволяет увидеть путь решения задачи. Конечно, для этого нужно знать фундамент геометрии и рубить в свойствах геометрических фигур (см. предыдущий пункт).

Четвёртое. Разработка алгоритма решения. Многие задачи геометрии являются многоходовыми, поэтому решение и его оформление очень удобно разбивать на пункты. Нередко алгоритм сразу же приходит в голову, после того как вы прочитали условие или выполнили чертёж. В случае возникновения трудностей начинаем с ВОПРОСА задачи. Например, по условию «требуется построить прямую…». Здесь самый логичный вопрос такой: «А что достаточно знать, чтобы построить данную прямую?». Предположим, «точка нам известна, нужно знать направляющий вектор». Задаём следующий вопрос: «Как найти этот направляющий вектор? Откуда?» и т.д.

Иногда случается «затык» – не решается задача и всё тут. Причины стопора могут быть следующими:

– Серьёзный пробел в элементарных знаниях. Иными словами, вы не знаете или (и) не видите какой-то очень простой вещи.

– Незнание свойств геометрических фигур.

– Задача попалась трудная. Да, так бывает. Нет смысла часами париться и собирать слёзки в платочек. Обратитесь за консультацией к преподавателю, сокурсникам или задайте вопрос на форуме. Причём, его постановку лучше сделать конкретной – о том участке решения, который вам не понятен. Клич в виде «Как решить задачу?» выглядит не очень-то… и, прежде всего, для вашей собственной репутации.

Этап пятый. Решаем-проверяем, решаем-проверяем, решаем-проверяем-даём ответ. Каждый пункт задачи выгодно проверять сразу после его выполнения. Это поможет немедленно обнаружить ошибку. Естественно, никто не запрещает быстренько прорешать задачу целиком, но возникает риск переписывать всё заново (часто несколько страниц).

Вот, пожалуй, все основные соображения, которыми целесообразно руководствоваться при решении задач.

Практическая часть урока представлена геометрией на плоскости. Примеров будет всего два, но мало не покажется =)

Пройдёмся по нити алгоритма, который я только что рассмотрел в своём маленьком научном труде:

Пример 1

Даны три вершины параллелограмма . Найти четвёртую вершину .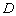

Начинаем разбираться:

Шаг первый: очевидно, что речь идёт о «плоской» задаче.

Шаг второй: в задаче речь идёт о параллелограмме. Все помнят такую фигуру параллелограмм? Не нужно улыбаться, немало людей получает образование в 30-40-50 и более лет, поэтому даже простые факты могут стереться из памяти. Определение параллелограмма встречается в Примере №3 урока Линейная (не) зависимость векторов. Базис векторов.

Шаг третий: Выполним чертёж, на котором отметим три известные вершины. Забавно, что несложно сразу построить искомую точку :

Построить, это, конечно, хорошо, но решение необходимо оформить аналитически.

Шаг четвёртый: Разработка алгоритма решения. Первое, что приходит в голову – точку можно найти как пересечение прямых 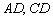. Их уравнения нам неизвестны, поэтому придётся заняться этим вопросом:

1) Противоположные стороны 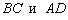параллельны. По точкам 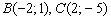найдём направляющий вектор данных сторон 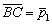. Это простейшая задача, которая рассматривалась на уроке Векторы для чайников.

Примечание: корректнее говорить «уравнение прямой, содержащей сторону», но здесь и далее для краткости я буду использовать словосочетания «уравнение стороны», «направляющий вектор стороны» и т.д.

2) Составим уравнение прямой 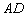по известной точке 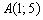и найденному направляющему вектору (см. статью Уравнение прямой на плоскости)

3) Противоположные стороны 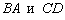параллельны. По точкам 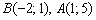найдём направляющий вектор этих сторон .

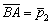4) Составим уравнение прямой 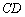по точке 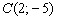и направляющему вектору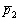

В пунктах 1-2 и 3-4 мы фактически дважды решили одну и ту же задачу, она, кстати, разобрана в примере №3 урока Простейшие задачи с прямой на плоскости. Можно было пойти более длинным путём – сначала найти уравнения прямых 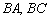и только потом «вытащить» из них направляющие векторы .

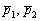5) Теперь уравнения прямых 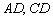известны. Осталось составить и решить соответствующую систему линейных уравнений (см. примеры №№4,5 того же урока Простейшие задачи с прямой на плоскости).

Точка 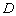найдена.

Задача довольно таки простая и её решение очевидно, но существует более короткий путь!

Второй способ решения:

Диагонали параллелограмма своей точкой пересечения делятся пополам. Точку 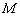я отметил, но чтобы не загромождать чертёж сами диагонали не провёл.

1) С помощью формул координат середины отрезка найдём точку 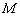– середину диагонали .

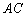2) Рассмотрим диагональ 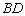. Из условия известна вершина «бэ», из предыдущего пункта найдена середина 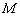. Используя те же формулы координат середины отрезка, находим вершину .

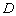Хорошее знание свойств параллелограмма позволило значительно сократить решение!

Желающие могут прорешать задачу. Всё перед глазами, все ссылки, комментарии даны. И, конечно, не забывайте про важный технический приём – решили пункт задания и сразу же его проверили (аналитически или по чертежу).

Переходим к наиболее распространённой задаче, которая встречается практически в каждом сборнике, в каждой методичке:

Date: 2015-04-23; view: 1116; Нарушение авторских прав