Как найти высоту треугольника?

5) Составим уравнение высоты 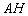и найдём её длину.

От строгих определений никуда не деться, поэтому придётся приворовывать из школьного учебника:

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

То есть, необходимо составить уравнение перпендикуляра, проведённого из вершины 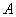к стороне 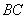. Данная задача рассмотрена в примерах №№6,7 урока Простейшие задачи с прямой на плоскости. Из уравнения 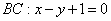снимаем вектор нормали 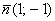. Уравнение высоты 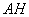составим по точке 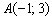и направляющему вектору :

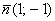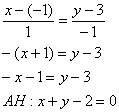
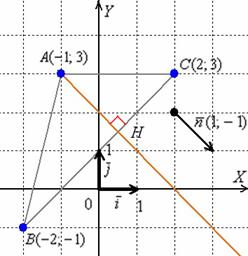
Обратите внимание, что координаты точки 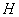нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: 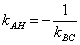. В данном случае 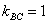, тогда: 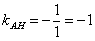. Уравнение высоты 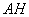составим по точке 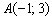и угловому коэффициенту 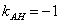(см. начало урока Уравнение прямой на плоскости):

Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим – точку пересечения высоты и стороны ;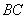
б) находим длину отрезка 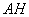по двум известным точкам.

Но на уроке Простейшие задачи с прямой на плоскости рассматривалась удобная формула расстояния от точки до прямой. Точка известна: 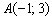, уравнение прямой тоже известно: 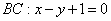, Таким образом:

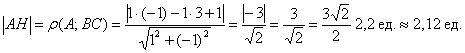
5) Вычислим площадь треугольника. В пространстве площадь треугольника традиционно рассчитывается с помощью векторного произведения векторов, но здесь дан треугольник на плоскости. Используем школьную формулу:
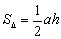– площадь треугольника равна половине произведения его основания на высоту.

В данном случае:

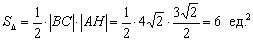
Date: 2015-04-23; view: 1380; Нарушение авторских прав