Решение и Способ первый

Рассмотрим две прямые, заданные уравнениями в общем виде:

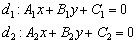
Если прямые не перпендикулярны, то ориентированный угол 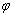между ними можно вычислить с помощью формулы:

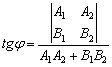
Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых:

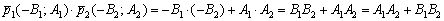
Если 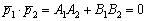, то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.

Исходя из вышесказанного, решение удобно оформить в два шага:

1) Вычислим скалярное произведение направляющих векторов прямых:
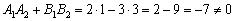, значит, прямые не перпендикулярны.

2) Угол между прямыми найдём по формуле:

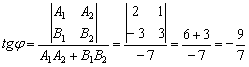
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса (см. Графики и свойства элементарных функций):

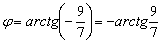
Ответ: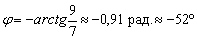

В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора.

Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация:

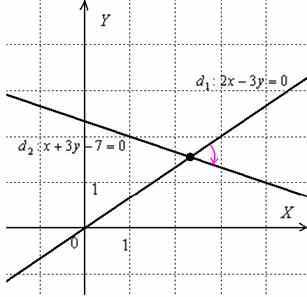
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи первым номером идёт прямая 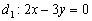и «открутка» угла началась именно с неё.

Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты 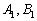взять из второго уравнения 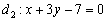, а коэффициенты 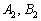взять из первого уравнения 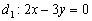. Короче говоря, начать необходимо с прямой .

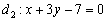Утаивать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.

Для проверки решения можно взять транспортир и измерить угол.

Date: 2015-04-23; view: 334; Нарушение авторских прав