Линейные пространства

4.1. Что называется линейным пространством? Приведите примеры линейных пространств.

4.2. Являются ли линейными пространствами:

а) множество геометрических радиус-векторов, оканчивающихся на данной плоскости;

б) множество всех сходящихся последовательностей; последовательностей, сходящихся к числу а; расходящихся последовательностей;

в) множество всех функций, дифференцируемых на интервале (a, b);

г) множество многочленов 3-й степени; степени не выше 3;

д*) множество всех положительных функций с операциями “сложения”: f (t)× g (t) и “умножения на число”: f (t)^a. Объясните результаты.

4.3. Что такое линейное подпространство? Являются ли линейными подпространствами соответствующих линейных пространств множества:

а) векторов из 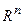, у которых сумма координат равна а; координаты с четными номерами совпадают; координаты - целые числа;

б) радиус-векторов плоскости, оканчивающихся в I четверти; в I или III четвертях;

в) всех функций, непрерывных на отрезке [ a, b ] и равных нулю на концах отрезка;

г) всех симметричных матриц n -го порядка?

4.4. Что называется линейной оболочкой системы векторов? Является ли она подпространством? Почему?

4.5. Дайте определение линейной зависимости системы векторов. Каков критерий линейной зависимости системы, состоящей из одного вектора; из двух векторов? Объясните свой ответ. Сформулируйте общий критерий линейной зависимости системы векторов.

4.6. Верно ли утверждение: если любые два вектора системы из n > 2 векторов линейно независимы, то и вся система линейно независима. Почему?

4.7. Верно ли утверждение: если система содержит вектор, который не выражается линейно через остальные векторы системы, то она линейно независима. Ответ обоснуйте.

4.8. Каков геометрический смысл линейной зависимости системы 2-х векторов; 3-х векторов? Существуют ли линейно независимые системы из 4-х и более геометрических векторов; а линейно зависимые?

4.9. Что такое ранг системы векторов, что такое максимальная линейно независимая подсистема? Как связаны ранги двух систем векторов, одна из которых линейно выражается через другую? Что происходит с рангом системы векторов при выполнении элементарных преобразований?

4.10. Что называется базисом n -мерного линейного пространства? Приведите примеры. Как определяются координаты вектора в данном базисе? Как выражаются линейные операции над векторами в координатах?

4.11. Что такое полная система векторов в линейном пространстве? Сформулируйте теорему об эквивалентном описании базиса как линейно независимой полной системы векторов.

4.12. Что является базисом линейной оболочки системы векторов и какова ее размерность?

4.13. Привести пример одномерного и двухмерного подпространств в пространстве: а) R ³; б) М ₂₃; в) P ₃.

Типовой расчет №2

Date: 2015-04-23; view: 975; Нарушение авторских прав