Алгебра матриц

3.1. Сформулируйте правило умножения матриц. Объясните, как изменится произведение АВ, если переставить i -ю и j -ю строки матрицы А; i -й и j -й столбцы матрицы В? Чему равна i -я строка АВ; j -й столбец АВ?

3.2. Покажите, что если АВ = ВА, то А и В - квадратные матрицы одного порядка. Верно ли обратное?

3.3. Верны ли формулы (А + В)²= А ² + 2 АВ + В ²; (А + В)(А - В) = А ² - В ² для квадратных матриц?

3.4. Что такое обратная матрица? Каков критерий ее существования, как она вычисляется? Выделите случай матриц 2-го порядка.

3.5. Чему равно произведение двух диагональных матриц? Как найти обратную матрицу для диагональной матрицы?

3.6. Как решить матричное уравнение вида АХВ = С, где Х - неизвестная матрица; А, В - невырожденные квадратные матрицы? Как получить отсюда решение уравнения АХ = С; уравнения ХВ = С?

3.7*. Верна ли формула (А ^-1)^Т=(А ^Т)^-1?

3.8. Пусть 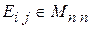- матрица, у которой на (i, j) месте стоит 1, а на остальных местах - нули. Доказать, что .

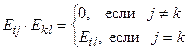3.9*. Привести пример ненулевой матрицы Х, удовлетворяющей условию Х ² = 0; условию Х ² = Х. Существуют ли такие примеры с det Х ¹ 0?

3.10*. Матрица Х удовлетворяет условию: а) Х ² = Е; б) Х ³ = Е. Чему может равняться det Х? Привести пример таких недиагональных матриц.

Date: 2015-04-23; view: 1202; Нарушение авторских прав