
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практические задания. Задача 1. Разложить многочлен
|
|
Задача 1. Разложить многочлен
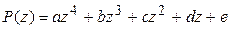
а) на линейные множители; б) на линейные и квадратичные множители с действительными коэффициентами.
| № вар. | a | b | c | d | e |
| -1 | -7 | -5 | -2 | ||
| -10 | -11 | -12 | |||
| -3 | |||||
| -8 | -2 | ||||
| -2 | -8 | ||||
| -5 | -3 | ||||
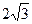
| |||||
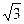
| 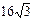
| ||||
- 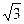
| |||||
| –3 | –8 | –9 | –5 | ||
| –3 | –4 | –4 | |||
| –2 | –4 | –8 | |||
| –7 | –18 | –18 | |||
| –3 | –5 | –21 | –20 | ||
| –1 | |||||
| –2 | |||||
| –1 | |||||
| –9 | |||||
Указания: 1) в вариантах 1-5, 16-20 найти целочисленные корни многочлена; 2) в вариантах 6-10, 21-25 известен корень z0:
| № вар. | |||
| z 0 | 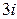
| 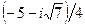
| 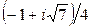
|
| № вар. | |||
| z 0 | 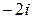
| 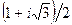
| 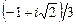
|
| № вар. | |||
| z 0 | 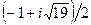
| 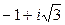
| 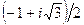
|
| № вар. | |||
| z 0 | 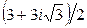
|
Задача 2. Пусть М - множество многочленов с вещественными коэффициентами P (t)Î Pn, удовлетворяющих указанным условиям. Доказать, что М - подпространство в Pn; найти базис и размерность М. Дополнить базис М до базиса Pn.
| № вар. | n | Условия на
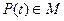
|
| P (-1) = P (1) | ||
| P ¢(-1) = P ¢(1) | ||
| P (-2) = 0 | ||
| P(-2) = P(3) = 0 | ||
| P (2 - i) = 0 | ||
| P ¢(1) = 0 | ||
| P (0) + P ¢(-1)=0 | ||
| P (i- 1) = 0 | ||
P (t) 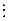 (t - 3)2 (t - 3)2
| ||
| P ¢¢(1) = 0 | ||
P (t) 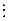 (t 2 + t + 1) (t 2 + t + 1)
| ||
| P (1) = P (2) = 0 | ||
| 2 P (0) + P (1) = 0 | ||
| P (-1) + P (0) + P (1) = 0 | ||
| P (0) + P ¢(2) = 0 | ||
| P (2) = P (–2) | ||
| P (1)= P ¢¢(0) = 0 | ||
| P (2) = 0 | ||
| P (2) = P ¢(0) = 0 | ||
| P (1 + i) = 0 | ||
| P ¢(–1) = 0 | ||
| P ¢(0) + P (1) = 0 | ||
| P (2 + i) = 0 | ||
| P (-1) = P ¢(–1) = 0 | ||
| P ¢¢(1) + P ¢(0) = 0 | ||
P (t) 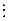 (t 2 +4 t + 5) (t 2 +4 t + 5)
| ||
| P (–1) + P ¢¢(0) = 0 | ||
| P (–1) = 2 P (0) | ||
| P (-1) + P ¢(0) + P (1) = 0 | ||
| P ¢¢(0) = P (–1) = 0 |
Задача 3. Найти размерность и построить базис линейного подпространства М в пространстве всех матриц данного размера (см. теоретические упражнения №5). Проверить, что матрица В принадлежит М, и разложить ее по базису в М.
| № вар. | М - множество матриц указанного вида | В |
Решения матричного уравнения 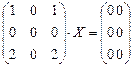
| 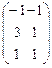
| |
Решения матричного уравнения 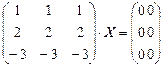
| 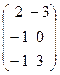
| |
Матрицы, перестановочные с матрицей А = 
| 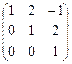
| |
Матрицы, перестановочные с матрицей А = 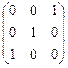
| 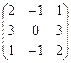
| |
Матрицы антиперестановочные с матрицей А = 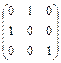
| 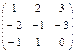
| |
Матрицы, антиперестановочные с матрицей
А = 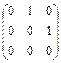
| 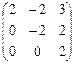
| |
| Симметричные матрицы 3-го порядка | 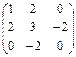
| |
| Кососимметричные матрицы 3-го порядка | 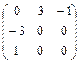
| |
| Верхнетреугольные матрицы 3-го порядка с нулевым следом | 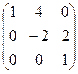
| |
| Матрицы 3-го порядка с нулевыми суммами элементов вдоль главной и побочной диагоналей | 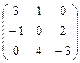
| |
| Матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца одинаковы | 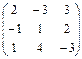
| |
| Матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца равны нулю | 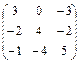
| |
Матрицы 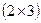 , у которых суммы элементов в обеих строках одинаковы , у которых суммы элементов в обеих строках одинаковы
| 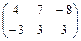
| |
Матрицы, перестановочные с матрицей А = 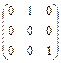
| 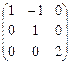
| |
Матрицы, антиперестановочные с матрицей А = 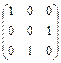
| 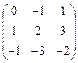
| |
Решения матричного уравнения 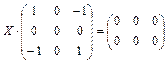
| 
| |
Решения матричного уравнения 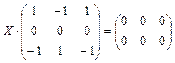
| 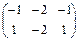
| |
Матрицы, перестановочные с матрицей А = 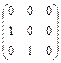
| 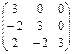
| |
Матрицы, перестановочные с матрицей А = 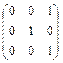
| 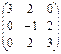
| |
Матрицы, антиперестановочные с матрицей А = 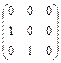
| 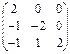
| |
Матрицы, антиперестановочные с матрицей А = 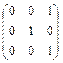
| 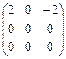
| |
| Симметричные матрицы 3-го порядка с нулевыми суммами элементов из первого и третьего столбцов | 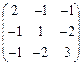
| |
| Кососимметричные матрицы 3-го порядка с нулевой суммой элементов из первой строки | 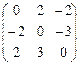
| |
| Нижнетреугольные матрицы 3-го порядка с нулевым следом и нулевой суммой элементов по побочной диагонали | 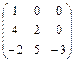
| |
| Симметричные матрицы 3-го порядка, у которых одинаковы суммы элементов в строках, а суммы элементов в столбцах знакочередуются | 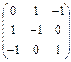
| |
| Симметричные матрицы 3-го порядка, у которых одинаковы суммы элементов в столбцах, а суммы элементов в строках знакочередуются | 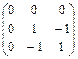
| |
| Симметричные матрицы 3-го порядка, у которых сумма элементов любого столбца равна 0 | 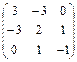
| |
Матрицы 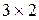 , у которых суммы элементов в обоих столбцах равны 0 , у которых суммы элементов в обоих столбцах равны 0
| 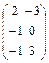
| |
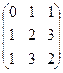
Симметричные матрицы,
перестановочные с матрицей
А = 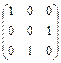
| 
| |
Симметричные матрицы, антиперестановочные с матрицей
А = 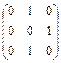
| 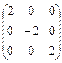
|
Задача 4*. Доказать, что множество М функций  , заданных на области D, образует линейное пространство. Найти его размерность и базис.
, заданных на области D, образует линейное пространство. Найти его размерность и базис.
| № вар | Множество М (a, b, g, d - любые вещественные числа) | D |
| 1, 18 | М = 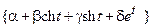
| 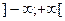
|
| 2, 19 | М = 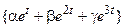
| 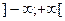
|
| 3, 20 | М = 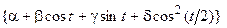
| 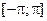
|
| 4, 21 | М = 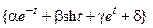
| 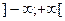
|
| 5, 22 | М = 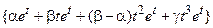
| 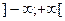
|
| 6, 23 | М = 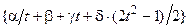
| 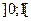
|
| 7, 24 | М = 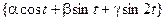
| 
|
| 8, 25 | М = 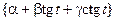
| 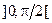
|
| 9, 26 | М = 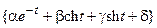
| 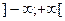
|
| 10, 27 | М = 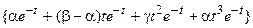
| 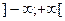
|
| 11, 28 | М = 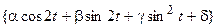
| 
|
| 12, 29 | М = 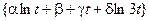
| 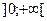
|
| 13, 30 | М = 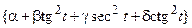
| 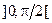
|
| 14, 16 | М = 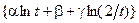
| 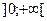
|
| 15, 17 | М = 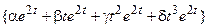
| 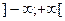
|
Контрольные вопросы
Date: 2015-04-23; view: 1733; Нарушение авторских прав