Линейные пространства (см. [2; гл.II §§3, 4], [3; гл. 4 §1], [4; гл.V §2])

4.1. Понятие линейного пространства. Аксиомы линейного пространства и следствия из них. Примеры линейных пространств (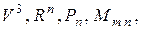 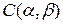). Линейное подпространство, линейная оболочка системы векторов.

4.2. Линейная зависимость и независимость системы векторов. Свойства линейной зависимости и независимости. Критерий линейной зависимости. Геометрический смысл линейной зависимости двух и трех геометрических векторов.

4.3. Ранг системы векторов. Определение ранга и базы для системы векторов. Линейная оболочка системы и ее базы, их совпадение. Сохранение ранга системы при добавлении к ней вектора из линейной оболочки. Критерий базы.

4.4. Сохранение ранга системы векторов при элементарных преобразованиях. Взаимосвязь рангов двух систем, когда векторы одной системы линейно выражаются через векторы другой. Элементарные преобразования системы векторов и сохранение ранга системы при их выполнении.

4.5. Базис и размерность линейного пространства. Определение базиса и размерности. Критерий базисности системы векторов (линейная независимость и полнота). Примеры линейных пространств и базисы в них (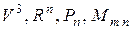). Пример бесконечномерного линейного пространства.

4.6. Координаты векторов в базисе. Однозначность разложения вектора по базису. Координаты вектора. Линейные операции над векторами в координатах.

4.7. Линейное подпространство и линейная оболочка системы векторов (как подпространство). Базис и размерность линейной оболочки и подпространства. Дополнение базиса подпространства до базиса линейного пространства.

Типовой расчет №2 охватывает следующие темы:

5. Теория систем линейных уравнений (см. [2; гл.1 §§9-11], [3; гл. 3 §§3,4],[4; гл.VII §§1-3]). 5.1. Ранг матрицы. Понятие ранга матрицы. Сохранение его при транспонировании. Теорема о базисном миноре. Критерий равенства определителя нулю. Совпадение ранга матрицы с рангом системы строк (столбцов) матрицы.

5.2. Приведение матрицы к ступенчатому и простейшему виду. Сохранение ранга матрицы при элементарных преобразованиях. Матрица ступенчатого вида и ее ранг. Приведение матрицы к ступенчатому виду (прямой ход метода Гаусса). Приведение ступенчатой матрицы к простейшему виду (обратный ход метода Гаусса).

5.3. Решение систем линейных уравнений методом Гаусса. Матрица системы и ее расширенная матрица. Элементарные преобразования системы и ее расширенной матрицы по методу Гаусса. Критерий совместности системы (теорема Кронекера–Капелли) и единственности решения.

5.4. Построение общего решения однородной системы. Критерий существования ненулевых решений однородной системы линейных уравнений (выделить случай квадратной системы). Линейное пространство решений однородной системы, его размерность и базис (фундаментальная система решений). Структура общего решения.

6. Линейные операторы (см. [2; гл. III, §§ 1-4, 6-9], [3; гл. IV, § 2], [4; гл. IX, §§ 5,6]). 6.1. Линейные операторы и их матрицы. Понятие линейного оператора, его свойства и примеры. Матрица линейного оператора в данном базисе. Векторно-матричная запись действия линейного оператора.

6.2. Действия с операторами и их матрицами. Умножение линейных операторов на число, сложение и умножение операторов. Соответствующие действия с матрицами операторов. Обратный оператор и обратная матрица.

6.3. Замена базиса. Матрица перехода от одного базиса к другому. Преобразование координат вектора при переходе к новому базису.

6.4. Матрицы линейного оператора в разных базисах. Преобразование матрицы линейного оператора при переходе к новому базису. Подобие матриц и его свойства. Инвариантность определителя матрицы линейного оператора при замене базиса.

6.5. Собственные значения и собственные векторы. Понятия собственного значения и собственного вектора линейного оператора, их общие свойства. Линейная независимость собственных векторов, отвечающих разным собственным значениям. Оператор простого типа, диагонализуемость его матрицы. Достаточное условие оператора простого типа. Пример оператора непростого типа.

6.6. Нахождение собственных значений и собственных векторов. Характеристический многочлен, нахождение собственных значений и собственных векторов с помощью характеристического уравнения. Инвариантность собственных значений, следа и определителя матрицы линейного оператора.

7. Билинейные и квадратичные формы (см. [2; гл. VI, §§1-5], [3; гл. IV, §3], [4; гл. IX, §§2-4]). 7.1. Билинейная форма и ее матрица. Понятие билинейной формы. Матрица формы. Координатная и векторно-матричная запись формы. Преобразование матрицы формы при замене базиса. Квадратичная форма, порожденная симметричной билинейной формой, ее координатная и векторно-матричная запись.

7.2. Приведение квадратичной формы к каноническому и нормальному виду. Канонический и нормальный вид квадратичной формы. Приведение формы к каноническому виду методом Лагранжа. Закон инерции квадратичных форм. Положительный и отрицательный индексы формы, ранг формы.

7.3. Знакоопределенная квадратичная форма, ее индексы и ранг. Критерий Сильвестра положительной (отрицательной) определенности квадратичной формы.

8. Евклидовы пространства (см. [2; гл. IV, §§1-3, гл. V, §§2-4], [3; гл. IV, §§1, 2], [4; гл. X, §§1-4]). 8.1. Евклидово пространство. Евклидово скалярное произведение. Примеры евклидовых пространств. Неравенство Коши–Буняковского. Длины векторов и углы между ними. Свойства длины вектора.

8.2. Матрица Грама. Матрица Грама скалярного произведения, его координатная и векторно-матричная записи. Критерий матрицы Грама. Преобразование матрицы Грама при замене базиса.

8.3. Ортонормированный базис. Линейная независимость ортогональной системы векторов. Ортогональный и ортонормированный базисы. Запись матрицы Грама, скалярного произведения, длины вектора в ортогональном и ортонормированном базисах. Метод ортогонализации базиса.

8.4. Сопряженные и самосопряженные операторы. Их матрицы.

8.5. Ортогональное преобразование. Его матрица, свойства. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.

Date: 2015-04-23; view: 874; Нарушение авторских прав