Учет колебаний с другими собственными частотами

Теоретические соображения, изложенные выше, справедливы не только для электронов, но и для ионов. Причём, для ионов классические представления более обоснованы, так как их массы значительно больше масс электронов. Во всех телах наблюдается не одна, а несколько полос поглощения, соответствующих различным затухающим гармоническим осцилляторам с их собственными частотами w_k. В газах, где можно пренебречь их взаимодействием, для квадрата показателя преломления получим

,

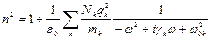где N_k, q_k, m_k, g_k, w_0k – концентрация, заряд, масса, коэффициент затухания и собственная частота осциллятора k -го типа.

Каждой собственной частоте соответствует своя полоса поглощения, вблизи которой показатель преломления меняется аномально. Общий ход показателя преломления n_R(w) в зависимости от частоты представлен схематически на рисунке

Из экспериментов по изучению полос поглощения исследуемого вещества можно найти коэффициенты C_k = N_kq_k²/m_k, откуда можно оценить удельные заряды q_k/m_k и природу осцилляторов. Так, в согласии с теорией, было найдено, что все осцилляторы чётко разделяются на две группы: у одной удельные заряды по порядку величины такие же, как у электронов, у другой – как у ионов. Первым соответствуют полосы поглощения, лежащие в ультрафиолетовой (реже – в видимой), вторым – в инфракрасной области спектра.

Подобный же ответ для движения электронов в атоме даёт и квантовая механика, но с учётом следующих особенностей. У атомов есть несколько собственных частот, каждая из которых имеет свою диссипативную постоянную g. Кроме того, каждая гармоника имеет ещё свою эффективную «силу», выражаемую в виде произведения поляризуемости при данной частоте на постоянную связи f, равную по порядку величины единице. Таким образом, для атомной поляризуемости в квантовой механике получим

,

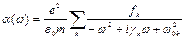где суммирование производится по всем гармоникам.

В теории для показателя преломления плотных материалов необходимо учесть, что на каждый атом вещества кроме поля волны действуют и другие поля, создаваемые соседними атомами, поляризованными той же волной. При условии, что длина волны много больше размера атома, для изотропного материала, а также в случае кубического кристалла, локальное поле возрастает на величину P /3e₀ по сравнению с полем волны E. В этом случае вектор поляризации P становится равным

.

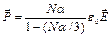Таким образом, для квадрата показателя преломления получится

.

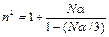Более удобно это выражение представить в виде

,

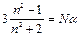известном как формула Клаузиуса – Моссотти.

В плотном материале возникает и другое усложнение. Поскольку атомы расположены слишком тесно, они сильно взаимодействуют друг с другом. При этом все собственные частоты w₀ и коэффициенты затухания g в атомной поляризуемости a(w) атомов твёрдого вещества будут другими, чем для свободных атомов. С этой оговоркой, по крайней мере, приближённо, формулу Клаузиуса – Моссотти можно представить следующим образом:

.

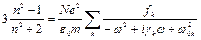И, наконец, последнее усложнение. Если плотный материал представляет собой смесь нескольких компонент, то каждая из них даёт свой вклад в поляризацию. Полная a(w) будет суммой вкладов различных компонент смеси. Тогда формула Клаузиуса – Моссотти примет вид

,

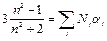где суммирование производится по всем компонентам смеси.

Показатель преломления n в этом выражении является комплексной функцией частоты w, поскольку таковой является средняя атомная поляризуемость a(w).

Date: 2015-05-05; view: 610; Нарушение авторских прав