Интерференция от двух точечных монохроматических источников света

Два точечных когерентных источника света можно получить путем деления волны от одного точечного источника на две части. Существует множество интерференционных схем такого разделения. Приведем некоторые из них.

Схема Юнга состоит из одного источника света и непрозрачного экрана с двумя отверстиями.

Согласно принципу Гюйгенса, каждую точку фронта волны, дошедшего до экрана,

можно рассматривать как источник вторичных волн. Поскольку отверстия расположены на фронте волны и воспроизводят одно и то же колебание, то они являются когерентными и синфазными источниками.

Бипризма Френеля представляет собой призму, сечением которой является равнобедренный треугольник с очень малыми углами при основании. Если на большую грань направить свет от источника S, то в результате двукратного преломления лучей, исходный пучок преобразуется в два пучка лучей, идущих от боковых граней бипризмы. Если падающий пучок достаточно узкий, то мнимые продолжения преломленных пучков пересекутся в двух точках. Эти точки два мнимых изображения S₁ и S₂ источника S. S₁ и S₂ являются источниками когерентных волн. Интерференция будет наблюдаться в области перекрытия пучков.

Зеркало Ллойда. Схема состоит из источника и зеркала. Происходит интерференция волн, одна из которых идет непосредственно от источника, а вторая от мнимого изображения источника в зеркале.

Особенность данной схемы в том, при отражении фаза волны меняется на противоположную, и к разности хода добавится . Кроме этого, интерференционная картина, полученная таким способом, имеет малую контрастность, так как интенсивность отраженной волны составляет всего несколько процентов от интенсивности падающей волны.

Существует еще ряд интерференционных схем, например бизеркала Френеля, билинза Бийе и т.д.

В интерференционных картинах приведенных выше схем, максимумы располагаются в тех точках, для которых в разности хода укладывается чётное число полуволн, а минимумы – в точках, для которых в разности хода укладывается нечетное число полуволн. Получается, что геометрическое положение, например, максимумов - это множество точек пространства, для каждой из которых разность расстояний до двух источников (точек) – константа. Вышесказанное является определением гиперболы. В случае максимумов интерференции этими константами являются значения 0, λ, 2λ, 3λ, 5λ. Т.е. в пространстве геометрическим положением максимумов является семейство гиперболоидов вращения с общими фокусами – когерентными источниками света. Если параллельно линии соединяющей источники расположить экран, то на нем будут наблюдаться чередующиеся светлые и темные полосы. Полосы – результат пересечения гиперболоида вращения и плоскости (рис. 2.3).

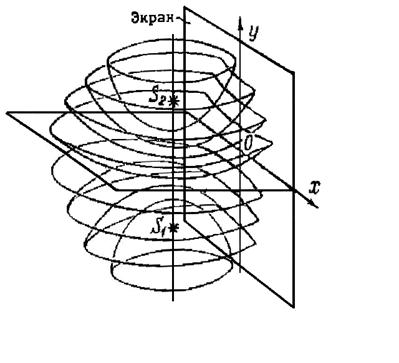
Рис.2.3.

Вопросы для самоконтроля

1. Какие источники света называются когерентными?
2. Что можно определить уравнением волны в выбранном направлении?
3. В чем суть метода векторной диаграммы сложения колебаний?
4. Что называют интерференционным членом?
5. Что называется оптической разностью хода?
6. Как связана оптическая разность хода и разность фаз?
7. Условия возникновения интерференционных максимумов и минимумов?
8. Что такое временнáя когерентность? Как она связана с разностью хода и разностью фаз?
9. Приведите примеры интерференционных схем?

Date: 2015-05-05; view: 1873; Нарушение авторских прав