
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифракция Фраунгофера на щели. Отклонения от закона прямолинейного распространения световых лучей, проявляющиеся при наличии препятствий на пути световой волны
|
|
Отклонения от закона прямолинейного распространения световых лучей, проявляющиеся при наличии препятствий на пути световой волны, называются дифракцией света. Возникающее при дифракции распределение интенсивности света в пространстве, называется дифракционной картиной.
Рассмотрим образование дифракционных максимумов и минимумов на экране при прохождении монохроматического света через щель шириной а (рис.3.1).

Рис.3. 1.
Согласно принципу Гюйгенса-Френеля, любая точка фронта волны является источником вторичных волн. Следовательно, дальнейшее направление распространения волны (луча) лежит в пределах от 0 до 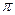 градусов.
градусов.
Собирающая линза является таутохронной системой, т.е. не оказывает влияния на изменение разности фаз между колебаниями, распространяющимися в параллельных направлениях.
Разность хода между крайними лучами
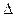 = а sinφ
= а sinφ  (3.1)
(3.1)
где φ- угол дифракции.
В любой точке пространства происходит сложение колебаний.
Рассмотрим точку О экрана. В точке О происходит сложение колебаний с нулевой разностью фаз с образованием максимума и результирующей амплитудой А 0. А 0 – результат сложения множества параллельных лучей с амплитудой Аi.
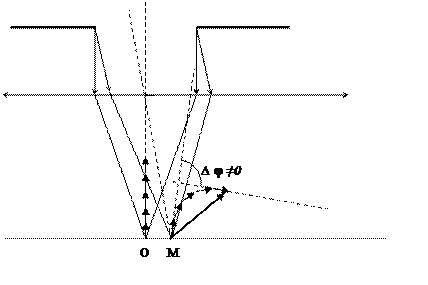
Рис.3.2.
Применим способ сложения колебаний с помощью векторной диаграммы. Пусть исходное направление вектора амплитуды Аi при значении угла дифракции φ равном 0 будет вертикально. Тогда вектор результирующей амплитуды А 0 будет представлять собой отрезок имеющий максимально возможную длину (рис.3.2).
Если рассмотреть некоторую другую точку экрана (например точку М), то каждый вектор Аi, вносящий свой вклад в образование результирующей амплитуды, будет повернут на некоторый угол по отношению к предыдущему (колебания будут отставать по фазе) и результирующий вектор будет короче. Первый вектор в точке М, разумеется, будет также повернут на некоторый угол по отношению к первому вектору в точке О, и этот угол также можно рассчитать зная ОМ, расстояние до экрана и длину волны. Но интенсивность в данной точке от этого не зависит и поэтому, для простоты мы будем изображать первый вектор произвольно. «Накопленная» разность фаз между первым и последним колебанием будет 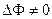 (рис.3.2). Разность фаз
(рис.3.2). Разность фаз 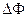 связана с разностью хода
связана с разностью хода 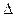 выражением
выражением
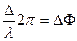 или
или 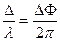 (3.2)
(3.2)
При 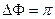 цепочка векторов Аi закручивается в полуокружность длины А 0 (рис.3.3).
цепочка векторов Аi закручивается в полуокружность длины А 0 (рис.3.3).

Рис.3. 3.
Произошло образование первого дифракционного максимума. Однако участок экрана от т. О до М будет освещен полностью. Причем в любой точке лежащей ближе к т. О освещенность будет больше чем в т. М, поскольку при одной и той же длине цепочки, длина результирующего вектора уменьшается (более подробно этот вопрос рассмотрен далее).
Когда 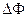 достигнет 2
достигнет 2 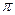 , то Арез =0, т.е. произойдет образование первого дифракционного минимума (рис.3. 4).
, то Арез =0, т.е. произойдет образование первого дифракционного минимума (рис.3. 4).
При дальнейшем увеличении 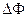 =2
=2 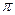 +
+ 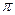 =3
=3 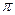 цепочка закручивается в спираль и происходит образование второго максимума.
цепочка закручивается в спираль и происходит образование второго максимума.
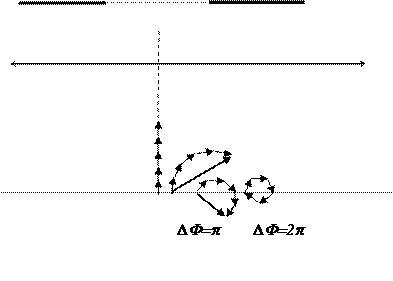

Рис.3.4.
Условия образования максимумов:
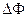 0=
0= 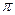 ;
; 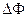 1 =3
1 =3 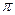 ;
; 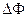 2 =5
2 =5 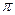 ;
; 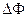 3 =7
3 =7 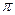 ;
;
(первый (первый (второй (третий
максимум) реальный реальный реальный
максимум) максимум) максимум)
В общем случае
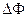 =(
=(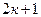 )
) 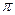 (3.3)
(3.3)
Решая совместно (3.1), (3.2) и (3.3) получаем:
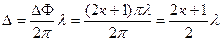
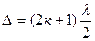
а sinφ = 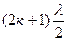 , к =0, 1, 2, 3 (3.4)
, к =0, 1, 2, 3 (3.4)
(3.4) – условие для максимумов.
Соответственно условие минимумов:
1) 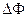 1 =2
1 =2 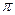 ;
;
2) 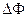 2 =4
2 =4 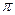 ;
;
3) 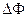 3 =6
3 =6 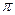 ;
;
n) 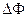 4 =2 к
4 =2 к 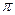 ; к = 1,2,3
; к = 1,2,3
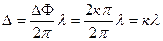
а sinφ = 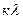 , где к =1,2,3,… (3.5)
, где к =1,2,3,… (3.5)
(3.5) – условие для минимумов освещенности на экране при дифракции на щели.
Date: 2015-05-05; view: 931; Нарушение авторских прав