Дифракционная решетка как спектральный прибор

Спектральным прибором называется устройство, которое позволяет произвести спектральный анализ светового потока, например, определить длины волн, входящие в его состав. К примеру, призма в результате дисперсии, разлагает свет в спектр и является основным компонентом спектрального прибора, который называется спектроскоп.

Дифракционная решетка также может играть роль спектрального прибора. Если источник света немонохроматический, то на экране появятся дифракционные картины созданные монохроматическими волнами, входящими в состав излучения источника.

Главные максимумы этой картины будут соответствовать условиям образования максимумов при сложении монохроматических волн, входящих в состав излучения источника.

d sinφ =m ,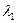

d sinφ =m ,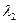

---------------

d sinφ =m .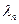

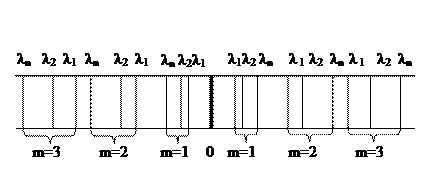
Рис.3.12.

На рисунке 3.12. представлена дифракционная картина от источника, в состав излучения которого входят волны с длинами 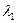, ,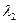…, 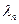.Причем, 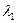< <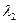…< 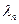. При дифракции Фраунгофера в центре экрана наблюдается яркий центральный максимум - выполняется условие максимума для всех волн. По мере удаления от центра вправо и влево, будут располагаться максимумы первого порядка, затем максимумы второго порядка и.т.д. Чем меньше длина волны, тем ближе к центру располагается соответствующий максимум. Совокупность максимумов первого порядка образует спектр первого порядка (m=1), совокупность максимумов второго порядка – спектр второго порядка (m=2) и.т.д. Спектры имеют разную ширину. Начиная с некоторого порядка, спектры начинают перекрываться. Перекрытие спектров затрудняет спектральный анализ. Максимальный интервал длин волн ∆λ, для которого спектры наблюдаются раздельно, называется дисперсионной областью. При использовании дифракционной решетки спектральный анализ обычно производится в спектрах не выше третьего. Дисперсионная область при этом оказывается очень большой - порядка нескольких тысяч ангстрем.

Следующей важной характеристикой спектрального прибора, является угловая дисперсия. Угловая дисперсия характеризует растянутость спектра. Угловой дисперсией спектрального прибора называют угловое расстояние ∆φ между линиями спектра, которые соответствуют длинам волн λ и λ+∆λ, различающимся на единицу длины. По определению угловая дисперсия D, есть

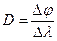. (3.18.)

Максимуму m – го порядка для длины волны λ соответствует угол φ. Поскольку, согласно (3.7)

d sinφ = m λ,

то максимуму того же порядка для близкой длины волны λ+∆λ будет соответствовать угол φ +∆φ. Связь между ∆λ и ∆φ получим, взяв дифференциал от обеих частей (3.7) при определенном m. Получим

d cosφ ∆φ = m ∆λ.

Отсюда используя определение (3.18.), получаем формулу для угловой дисперсии решетки:

. (3.19)

Угловая дисперсия увеличивается с ростом порядка дифракционного спектра и обратно пропорциональна периоду решетки. Таким образом, уменьшая период решетки, можно растянуть дифракционный спектр.

Однако при одинаковой дисперсии форма спектральных линий может быть различна. Одна из основных задач спектроскопии заключается в том, чтобы различать линии, соответствующие близким значениям длин волн.

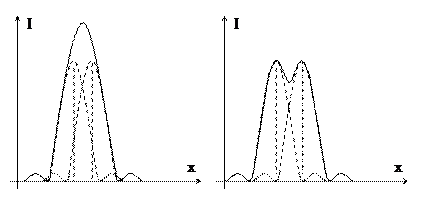
Рис. 3.13.

На рисунке 3.13. изображено распределение интенсивности в двух соседних спектральных линиях различных случаях. Пунктирные линии показывают распределение в каждой линии в отдельности, а сплошная – результирующее распределение интенсивности. В первом случае линии сливаются, а во втором их можно различить или «разрешить», т.к. между максимумами есть заметный перепад интенсивности. Чем больше перепад интенсивности, тем уже линии. Чем уже линии, тем лучше разрешаются близкие длины волн, соответствующие этим линиям. Величина, характеризующая способность спектрального прибора разрешать близкие длины волн, называется разрешающей способностью.

Разрешающая способность R равна отношению длины волны λ, в области которой ведется исследование к δλ – минимальной разности длин волн, при которой спектральные линии воспринимаются еще раздельно. Разрешимы линии или нет, определяют согласно критерию Рэлея. По Рэлею линии считаются разрешимыми, если максимум одной приходится на минимум соседней линии (рис.3.12. справа). При этом интенсивность в провале составляет около 80% от интенсивности в максимуме и линии воспринимаются раздельно.

Напомним, что минимум образуется каждый раз, когда разность фаз ∆Ф _N от крайних лучей становится равной n2π где n – номер минимума. Получается, что главный максимум в спектре m – го порядка это по сути m N - ый минимум (N- число штрихов). Тогда ближайший минимум n=m N +1. Если на этот минимум приходится максимум соответствующий длине волны λ+δλ, то λ и λ+δλ можно разрешить.

Итак, условие образования минимума

∆Ф _N = n2π,

Поскольку разность хода от соседних лучей 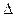= N d sinφ и связана с разностью фаз выражением

,

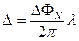то для образования любого n-го минимума должно выполняться следующее условие:

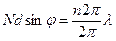или

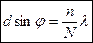. (3.20)

если n=m N - то наблюдаем максимум, если n=m N +1- наблюдаем ближайший минимум. Пусть под некоторым углом φ для длины волны λ+δλ наблюдается максимум, и под этим же углом наблюдается минимум для длины волны λ, тогда согласно критерию Рэлея соответствующие спектральные линии разрешимы и

.

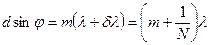Следовательно, разрешающая способность дифракционной решетки

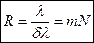. (3.21)

Вопросы для самоконтроля.

1. Что называется спектральным прибором?

2. Объясните механизм образования спектров?

3. Что называется дисперсионной областью?

4. Что называется угловой дисперсией?

5. Что называется разрешающей способностью?

6. Критерий Релея.

7. Формула угловой дисперсии.

8. Формула разрешающей способности.

Date: 2015-05-05; view: 2006; Нарушение авторских прав