Тема 2. Интерференция

Рассмотрим произвольную точку в области пространства, куда приходят возмущения от всех источников, т.е. место, где происходит наложение волн, и будем интересоваться интенсивностью света в данной точке пространства. Теория и опыт показывают, что во многих случаях имеет место суперпозиция интенсивностей: если I₁, I₂, … – интенсивности в точке наблюдения от каждого из источников (первого, второго, и т.д. соответственно), то полная интенсивность равна их сумме

.

В таком случае говорят, что интерференция отсутствует. Такая ситуация возникает в оптике при наложении волн от независимых источников.

Предположим, теперь, что источники (для простоты пусть их всего два – S₁ и S₂) испускают монохроматические волны одинаковой частоты. Тогда в каждую точку пространства (например, в точку В) будут приходить два гармонических колебания Е₁ и Е₂ (рис 2.1).

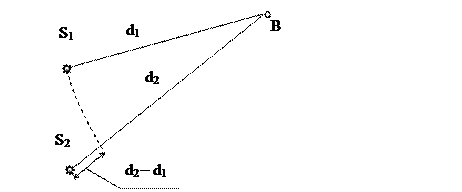
Рис. 2.1.

Пусть начальные фазы источников равны нулю. Тогда в точке B под действием источника S₁ возникает переменное электрическое поле, напряжённость Е₁ которого равна:

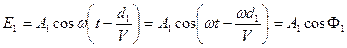, (2.1)

а от источника S₂:

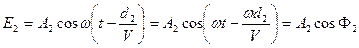. (2.2)

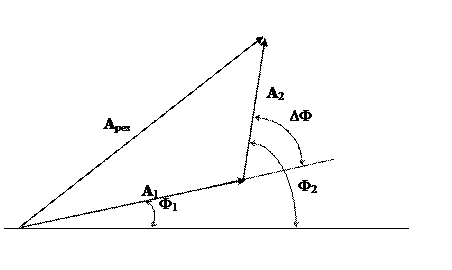В точке В складываются два колебания с амплитудами А₁ и А_2. Результат сложения можно изобразить на векторной диаграмме в виде суммы двух векторов, модули которых равны амплитудам, а углы между этими векторами и некоторым фиксированным направлением равны фазам F₁ и F₂ в данный момент времени (рис. 2.2).

Из полученного треугольника векторов можно найти вектор результирующей амплитуды А_рез. Согласно теореме косинусов, имеем:

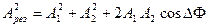. (2.3)

Поскольку интенсивность пропорциональна квадрату амплитуды, то можно записать

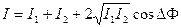(2.4)

Из выражения (2.4) видно, что суперпозиция интенсивностей не имеет места. Результирующая интенсивность зависит от последнего слагаемого 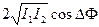, которое называют интерференционным членом. При этом распределение интенсивности в пространстве (обычно характерное чередование максимумов и минимумов) называют полем интерференции или интерференционной картиной.

Date: 2015-05-05; view: 469; Нарушение авторских прав