Проверка гипотезы о равенстве математических ожиданий двух генеральных совокупностей

Пусть и — две генеральные совокупности с известными дисперсиям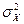и и 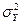и неизвестными математическими ожиданиям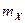и и . Из генеральных совокупностей взяты две независимые выборк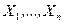и и и вычислены выборочные математические ожидания (средние) и 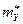. Для проверки гипотезы о равенстве математических ожиданий используют статистику

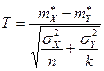, (9.3.1)

которая при выполнении нулевой гипотезы имеет нормальное распределение с параметрами .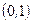

При неизвестных дисперсиях генеральных совокупностей либо требуется достаточно большой объем выборки для надежной и точной оценки, либо требуется, чтобы эти дисперсии были одинаковы, в противном случае известные критерии малоэффективны. Если дисперсии генеральных совокупностей равны 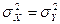, то для проверки нулевой гипотезы , используют статистику

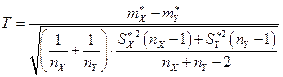, (9.3.2)

имеющую 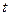‑ распределение (распределение Стьюдента) с 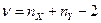степенями свободы.

Выбор критической области зависит от вида альтернативной гипотезы:

§ при альтернативной гипотезе необходимо выбрать правостороннюю критическую область;

§ при альтернативной гипотезе 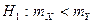необходимо выбрать левостороннюю критическую область;

§ при альтернативной гипотезе 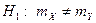необходимо выбрать двустороннюю критическую область.

Пример 2. Средний ежедневный объём продаж за I квартал 2004 года для 17 торговцев района A составляет 15 тысяч рублей при “исправленном” среднем квадратичном отклонении 2,5 тысяч рублей, а для 10 торговцев района B — 13 тысяч рублей при «исправленном» среднем квадратичном отклонении 3 тысячи рублей. Существенно ли различие в объёме продаж в районах A и B при 5%–м уровне значимости.

m Решение. Решим задачу, предположив, что ежедневный объём продаж подчинён нормальному закону при неизвестных параметрах распределения. Предположим, что дисперсии объёмов продаж одинаковы. Найдём критическую область для нулевой гипотезы при альтернативной гипотез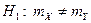е , где 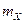— математическое ожидание объема продаж для района A, а — для района В.

В качестве критерия необходимо использовать функцию

,

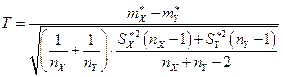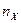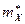где и объемы выборок, а и 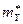оценки параметров 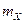и .

Функция имеет 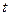‑ распределение (распределение Стьюдента) с 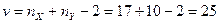степенями свободы.

По таблице 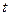– распределения для 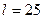и 5%‑го уровня значимости (для двусторонней критической области) находим:

, .

Это означает, что критической областью является .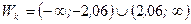

Вычислим :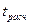

.

Полученное значение критерия 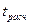не принадлежит критической области, следовательно, гипотеза принимается. l

Date: 2015-06-07; view: 961; Нарушение авторских прав