Доверительный интервал для дисперсии генеральной совокупности, имеющей нормальное распределение при известном математическом ожидании

Предположим, что выборка 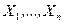произведена из нормальной генеральной совокупности с неизвестной дисперсией при известном математическом ожидании, равном 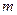. В качестве оценки неизвестной дисперсии 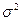возьмем выборочную дисперсию

. (8.4.11)

В этом случае статистика 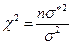будет иметь 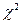–распределение с 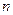степенями свободы.

Доверительный интервал для дисперсии при известном математическом ожидании имеет вид:

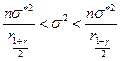, (8.4.12)

где 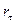— квантиль уровня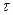 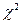–распределения с 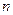степенями свободы.

Таким образом, доверительный интервал для дисперсии при известном математическом ожидании строится следующим образом:

1. Используя выборку 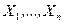, по формуле (8.4.11) вычисляем оценку дисперсии.

2. Вычисляем квантил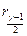и и 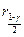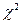–распределения с 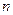степенями свободы.

3. По формуле (8.4.12) получаем искомый доверительный интервал.

Замечание. Квантил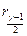и и 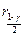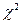–распределения с 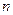степенями свободы можно определить разными способами, например:

§ используя таблицы 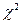–распределения с 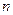степенями свободы;

§ используя функцию ХИ2ОБР (вероятность;степени_свободы) из EXCEL, при этом аргумент «вероятность» данной функции должен быть равен уровню значимости, а аргумент «степени_свободы» должен быть равен ;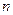

§ используя функцию qchisq(p, d) из MATHCAD, при этом переменные данной функции должны быть равны: .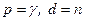

Аналогично строится доверительный интервал для дисперсии генеральной совокупности, имеющей нормальное распределение при неизвестном математическом ожидании.

В качестве оценки неизвестной дисперсии 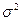возьмем выборочную дисперсию

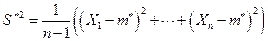. (8.4.13)

В этом случае статистика 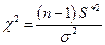будет иметь 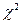–распределение с 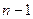степенью свободы.

Доверительный интервал для дисперсии при неизвестном математическом ожидании имеет вид:

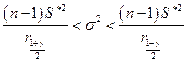, (8.4.14)

где 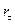— квантиль уровня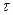 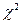–распределения с 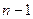степенью свободы.

Таким образом, доверительный интервал для дисперсии при неизвестном математическом ожидании строится следующим образом:

1. Вычисляем оценку 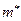, которая является средним арифметическим элементов выборки 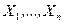, и по формуле (8.4.13) вычисляем выборочную оценку дисперсии.

2. Вычисляем квантил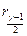и и 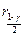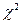–распределения с 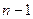степенью свободы.

3. По формуле (8.4.14) получаем искомый доверительный интервал.

Пример 5. Найти доверительный интервал с доверительной вероятностью 0,95 для оценки математического ожидания, нормально распределенной случайной величины , если известны ее дисперсия 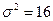, выборочная средняя 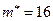и объем выборки .

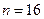m Решение. По условию задачи 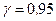. Найдем квантиль 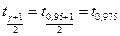нормального распределения с параметрами 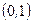, используя, например EXCEL: применяя функцию НОРМСТОБР(0,975), получим .

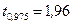Применив (8.4.6), получим

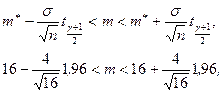
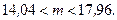l

Пример 6. Случайная величина распределена по нормальному закону. Статистический ряд выборки представлен таблицей:

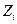
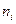
Требуется:

1) построить доверительный интервал для оценки математического ожидания, если доверительная вероятность равна 0,97;

2) построить доверительный интервал для оценки дисперсии, если доверительная вероятность равна 0,95.

m Решение. Для оценки математического ожидания будем использовать формулу (8.4.9), т.к. дисперсия неизвестна. Вычислим все величины, присутствующие в (8.4.9).

Объем выборки .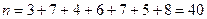

Оценка математического ожидания:

.

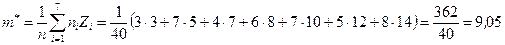Исправленная выборочная дисперсия:

.

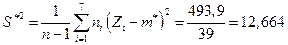Корень квадратный исправленной выборочной дисперсии:

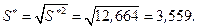
Для доверительной вероятности 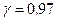найдем квантиль 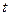‑распределения) с 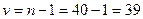числом степеней свободы. Для этого используем, например, функцию qt(p, d) из MATHCAD: .

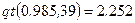Доверительный интервал имеет вид:

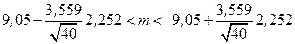
и окончательно

.

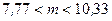Перейдем ко второй части задачи. Для оценки дисперсии будем использовать формулу (8.4.14), т.к. математическое ожидание неизвестно. Для данной формулы необходимо вычислить квантил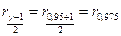и и 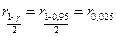. Используя функцию qchisq(p, d) из MATHCAD, получим: 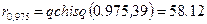и .

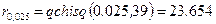Доверительный интервал имеет вид:

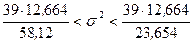
и окончательно

. l

Date: 2015-06-07; view: 1905; Нарушение авторских прав