
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Схема проверки нулевой гипотезы
|
|
1. По выборке 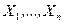 строят статистический ряд; он может быть как дискретным, так и интервальным. Рассмотрим для определенности интервальный ряд:
строят статистический ряд; он может быть как дискретным, так и интервальным. Рассмотрим для определенности интервальный ряд:
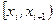
| 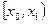
| 
| … | 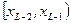
| 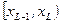
|
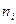
| 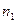
| 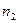
| … | 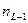
| 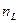
|
2. По данным предыдущих исследований или по предварительным данным делают предположение (выдвигают гипотезу) о модели закона распределения генеральной совокупности  .
.
Для предположения модели закона распределения генеральной совокупности  можно использовать графическое представление выборки.
можно использовать графическое представление выборки.
3. Используя выборочные данные, строят оценки параметров выбранной модели закона распределения.
4. Определяют теоретические вероятности попадания случайной величины в интервалы 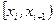 по формуле
по формуле
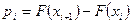 , (9.6.1)
, (9.6.1)
где 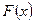 — предполагаемая функция распределения генеральной совокупности
— предполагаемая функция распределения генеральной совокупности  .
.
4. Определяют расчетное значение критерия К. Пирсона по формуле
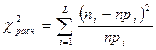
или
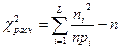 .
.
5. Выбрав уровень значимости 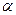 , находят критическую область (она всегда правосторонняя)
, находят критическую область (она всегда правосторонняя) 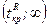 . Границу критической области можно найти одним из следующих:
. Границу критической области можно найти одним из следующих:
§ используя таблицы 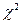 –распределения с
–распределения с  степенями свободы;
степенями свободы;
§ используя функцию ХИ2ОБР (вероятность;степени_свободы) из EXCEL, при этом аргумент «вероятность» данной функции должен быть равен уровню значимости, а аргумент «степени_свободы» должен быть равен  ;
;
§ используя функцию qchisq(p, d) из MATHCAD, при этом переменные данной функции должны быть равны: 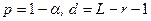 .
.
6. Если расчетное значение 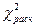 попадает в критическую область
попадает в критическую область 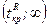 , то нулевая гипотеза
, то нулевая гипотеза 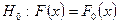 отвергается и принимается альтернативная гипотеза.
отвергается и принимается альтернативная гипотеза.
Замечание. При применении критерия К. Пирсона в каждом интервале должно быть не менее 5 элементов выборки (т.е. 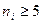 ). Если это условие не выполняется, то число интервалов надо уменьшить путем объединения соседних интервалов.
). Если это условие не выполняется, то число интервалов надо уменьшить путем объединения соседних интервалов.
Пример 5. Получены значения случайной величины  .
.
| 0,54 | 0,7 | 0,66 | 0,55 | 0,57 | 0,56 | 0,62 | 0,65 | 0,5 | 0,67 |
| 0,66 | 0,58 | 0,57 | 0,53 | 0,53 | 0,53 | 0,46 | 0,72 | 0,41 | 0,55 |
| 0,6 | 0,61 | 0,45 | 0,55 | 0,63 | 0,6 | 0,53 | 0,51 | 0,59 | 0,57 |
| 0,59 | 0,64 | 0,66 | 0,56 | 0,59 | 0,58 | 0,55 | 0,55 | 0,53 | 0,53 |
| 0,41 | 0,54 | 0,45 | 0,61 | 0,46 | 0,52 | 0,59 | 0,63 | 0,4 | 0,69 |
| 0,53 | 0,48 | 0,41 | 0,57 | 0,6 | 0,57 | 0,56 | 0,56 | 0,42 | 0,6 |
| 0,54 | 0,59 | 0,56 | 0,5 | 0,46 | 0,62 | 0,57 | 0,42 | 0,72 | 0,47 |
| 0,47 | 0,44 | 0,52 | 0,62 | 0,64 | 0,41 | 0,51 | 0,4 | 0,49 | 0,67 |
| 0,52 | 0,58 | 0,65 | 0,42 | 0,68 | 0,53 | 0,65 | 0,59 | 0,43 | 0,61 |
| 0,56 | 0,62 | 0,7 | 0,49 | 0,7 | 0,55 | 0,5 | 0,52 | 0,71 | 0,48 |
Необходимо:
1. Найти выборочные характеристики: выборочное среднее и исправленную выборочную дисперсию.
2. Построить доверительной вероятностью 0,95 доверительные интервалы для математического ожидания и дисперсии.
3. Построить гистограмму.
4. Проверить гипотезу о нормальном распределении случайной величины  при уровне значимости
при уровне значимости 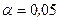 .
.
m Решение. Учитывая, что количество значений равно 100, определяем выборочное среднее и исправленную выборочную дисперсию:
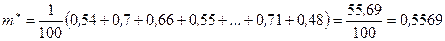 .
.
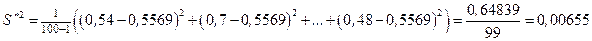 .
.
Замечание. Выборочное среднее можно определить используя функцию СРЗНАЧ(число1; число2;...) из EXCEL, а исправленную выборочную дисперсию можно определить используя функцию ДИСП(число1;число2;...) из EXCEL.
Перейдем к построению доверительных интервалов. При построении доверительного интервала для математического ожидания считаем, что при этом дисперсия не известна. Как известно из предыдущей главы, необходимо использовать формулу
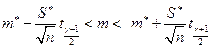 ,
,
в которой неизвестна только величина 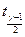 , являющаяся квантилем
, являющаяся квантилем 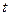 –распределения с
–распределения с 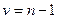 числом степеней свободы. Для доверительной вероятност и
числом степеней свободы. Для доверительной вероятност и 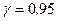 найдем квантиль
найдем квантиль 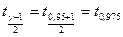
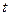 ‑распределения с
‑распределения с 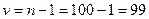 числом степеней свободы. Для этого используем, например, функцию qt(p, d) из MATHCAD:
числом степеней свободы. Для этого используем, например, функцию qt(p, d) из MATHCAD: 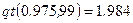 или функцию СТЬЮДРАСПОБ(вероятность; степени_свободы) из EXCEL:
или функцию СТЬЮДРАСПОБ(вероятность; степени_свободы) из EXCEL: 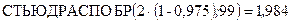 или Приложение 5.
или Приложение 5.
Определяем точность оценки
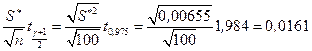 .
.
Таким образом, получаем доверительный интервал
 .
.
Построим доверительный интервал для дисперсии при неизвестном математическом ожидании. В этом случае необходимо использовать формулу
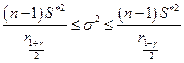 ,
,
где 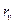 — квантиль уровня
— квантиль уровня 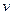
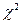 –распределения с
–распределения с 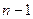 степенью свободы.
степенью свободы.
Для данной формулы необходимо вычислить квантили 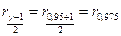 и
и 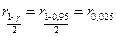 . Используя функцию qchisq(p, d) из MATHCAD, получим:
. Используя функцию qchisq(p, d) из MATHCAD, получим: 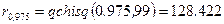 и
и 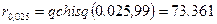 . Аналогичный результат можно получить используя функцию ХИ2ОБР (вероятность;степени_свободы) из EXCEL:
. Аналогичный результат можно получить используя функцию ХИ2ОБР (вероятность;степени_свободы) из EXCEL: 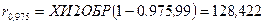 ,
, 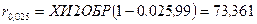 .
.
Таким образом, получаем доверительный интервал
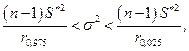
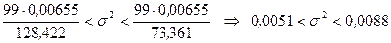 .
.
Перейдем к построению гистограммы. Построим интервальный ряд. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда): 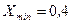 и
и 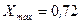 . Для нахождения минимального и максимального значений случайной величины можно использовать функции МИН(число1;число2;...) и МАКС(число1;число2;...) из EXCEL. Размах варьирования будет равен
. Для нахождения минимального и максимального значений случайной величины можно использовать функции МИН(число1;число2;...) и МАКС(число1;число2;...) из EXCEL. Размах варьирования будет равен 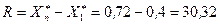 .
.
Возьмем число частичных интервалов 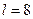 . В этом случае длина частичного интервала равна
. В этом случае длина частичного интервала равна
 .
.
Соответствующий интервальный ряд приведен в таблице 9.2.
Таблица 9.2
Номер
интервала
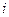
| Средний пробег автомобилей
(интервалы)
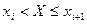
| Частота
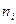
| Относительная частота
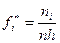
|
| 0,4 — 0,44 | 2,5 | ||
| 0,44 — 0,48 | |||
| 0,48 — 0,52 | 2,25 | ||
| 0,52 — 0,56 | 5,25 | ||
| 0,56 — 0,6 | 5,25 | ||
| 0,6 — 0,64 | 3,25 | ||
| 0,64 — 0,68 | 2,5 | ||
| 0,68 — 0,72 |
Гистограмма приведена на рис 9.4.
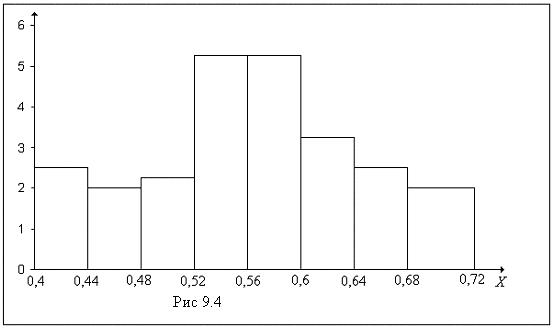
Проверим гипотезу о распределении случайной величины  . Найдем теоретические вероятности попадания случайной величины в интервалы
. Найдем теоретические вероятности попадания случайной величины в интервалы 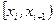 по формуле
по формуле 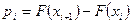 , где
, где 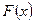 — функция распределения нормального закона. Так как случайная величина
— функция распределения нормального закона. Так как случайная величина  , подчиненная нормальному закону распределения, определена на
, подчиненная нормальному закону распределения, определена на 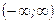 , то крайние интервалы в ряде распределения следует заменить на
, то крайние интервалы в ряде распределения следует заменить на 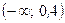 и
и 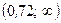 . Тогда
. Тогда
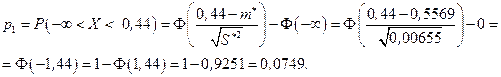
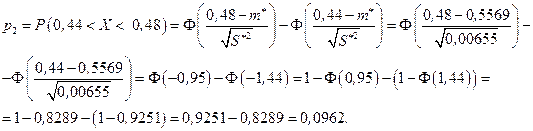
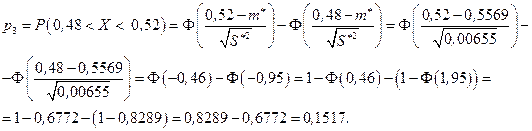
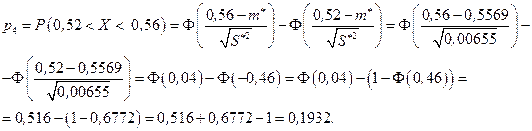
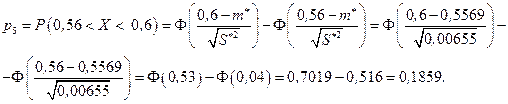
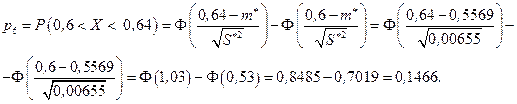
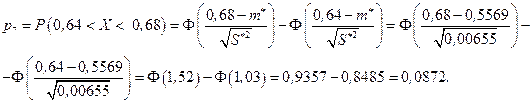
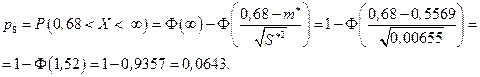
Дальнейшие вычисления удобно оформить в виде таблицы (табл. 9.3).
Таблица 9.3
| Номер интервала i | средний пробег автомобилей
(интервалы) 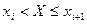
| Частота
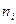
| Теоретические частоты
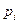
| 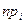
| 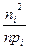
| |
| 0,4 — 0,44 | 0,0749 | 7,49 | 13,3511 | |||
| 0,44 — 0,48 | 0,0962 | 9,62 | 6,6528 | |||
| 0,48 — 0,52 | 0,1517 | 15,17 | 5,3395 | |||
| 0,52 — 0,56 | 0,1932 | 19,32 | 22,8261 | |||
| 0,56 — 0,6 | 0,1859 | 18,59 | 23,7224 | |||
| 0,6 — 0,64 | 0,1466 | 14,66 | 11,5280 | |||
| 0,64 — 0,68 | 0,0872 | 8,72 | 11,4679 | |||
| 0,68 — 0,72 | 0,0643 | 6,43 | 9,9533 | |||
| Итого | 104,8411 |
Определяем расчетное значение критерия К. Пирсона:
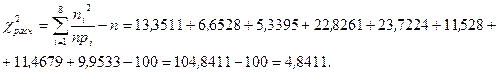
Находим число степеней свободы. По выборке были рассчитаны два параметра, значит, 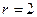 . Количество интервалов 8,т.е.
. Количество интервалов 8,т.е. 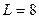 . Следовательно,
. Следовательно, 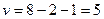 . Зная, что
. Зная, что 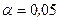 и
и 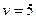 , находим границу правосторонней критической области
, находим границу правосторонней критической области 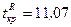 (см. Приложение 4). Таким образом, критической областью является интервал
(см. Приложение 4). Таким образом, критической областью является интервал 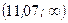 .
.
Так как расчетное значение критерия К. Пирсона  не попадает в критическую область, то нет оснований отвергнуть проверяемую гипотезу о нормальном законе распределения. l
не попадает в критическую область, то нет оснований отвергнуть проверяемую гипотезу о нормальном законе распределения. l
Date: 2015-06-07; view: 715; Нарушение авторских прав