Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Проверка гипотезы о значении дисперсии генеральной совокупности
|
|
Пусть 
— генеральная совокупность, распределенная по нормальному закону с неизвестной дисперсией 
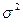. Из генеральной совокупности взята случайная выборка 
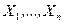и вычислена выборочная дисперсия 
.
Требуется проверить нулевую гипотезу 
, где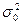 
— заданное значение дисперсии генеральной совокупности. Для проверки нулевой гипотезы используют статистику
, (9.4.1)
которая при выполнении нулевой гипотезы 
имеет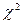 
‑распределение с 
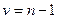степенями свободы.
Границы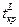 
и 
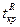критической области определяем по таблицам 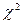‑распределения с 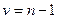степенями свободы или используя функцию ХИ2ОБР (вероятность; степени_свободы) из EXCEL, или используя функцию qchisq(p, d) из MATHCAD.
Пример 3. Точность работы автоматической линии проверяют по дисперсии контролируемого размера, которая не должна превышать 0,1 мм2. По результатам выборочного контроля получены следующие данные:
Контролируемый размер,  , мм2
| 43,0 | 43,5 | 43,8 | 44,4 | 44,6 |
Частота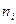 
|
Требуется проверить при уровне значимости 0,01, обеспечивает ли линия требуемую точность.
m Решение. Задача состоит в проверке гипотезы о значении дисперсии 
при альтернативной гипотезе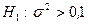 
. Таким образом, необходимо построить правостороннюю критическую область. Расчетное значение критерия вычисляем по формуле 
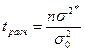, следовательно, по данным статистического ряда необходимо вычислить выборочную дисперсию. Дальнейшие вычисления удобно оформить в виде таблицы:
| № |
|
| 
| 
| 
| 
|
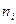
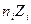
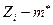
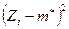
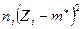
| 43,0 | 129,0 | -0,863 | 0,745 | 2,236 | ||
| 43,5 | 304,5 | -0,363 | 0,132 | 0,924 | ||
| 43,8 | 438,0 | -0,063 | 0,004 | 0,040 | ||
| 44,4 | 355,2 | 0,537 | 0,288 | 2,304 | ||
| 44,6 | 89,2 | 0,737 | 0,543 | 1,085 | ||
| Итого | 1315,9 | 6,590 | ||||
| Среднее | 43,863 | 0,220 |
; 
;
.
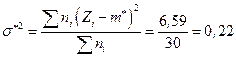Из условия 
, при числе степеней свободы равным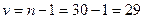 
находим границу правосторонней критической области. По таблице 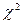‑ распределения получаем 
.
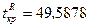Заметим, что аналогичный результат можно получить с помощью EXCEL или MATHCAD: 
или 
.
Это означает, что критической областью является 
. Очевидно, что расчетное значение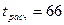 
находится внутри критической области, следовательно, нулевая гипотеза отвергается, т.е. автоматическая линия не обеспечивает заданную точность и требуется ее регулировка. l
Date: 2015-06-07; view: 755; Нарушение авторских прав