Теорема умножения вероятностей для нескольких событий

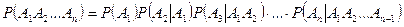. (3.2.4)

Пример 2. Бросают две монеты. Рассматриваются два события:

A — выпадение «герба» на первой монете;

B — выпадение «герба» на второй монете.

Найти вероятность события .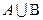

m Решение. Очевидно, что пространство элементарных исходов состоит из четырех исходов: «герб»‑«герб», «герб»‑«решка», «решка»‑«герб», «решка»‑«решка».

Применим теорему сложения вероятностей .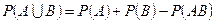

Очевидно, что и 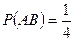, так как событию 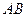благоприятствует всего один исход, а число возможных исходов равно 4. Окончательно получим:

.

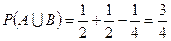Заметим, что задачу можно решить с помощью противоположного события. Рассмотрим событие — выпадение пары «решка»‑«решка», тогда

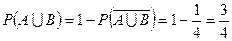. l

Пример 3. В урне 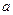белых и 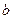черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

m Решение. Рассмотрим события:

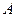— первый шар белый;

— второй шар белый.

Применяя теорему умножения вероятностей, получаем:

.

, так как общее число шаров, а также число белых, уменьшилось на 1. l

Пример 4. На семи карточках написаны буквы, образующие слово «телефон». После перестановки карточек наудачу последовательно берут пять из них, и прикладывают справа одну к другой. Найти вероятность образования слова «фенол».

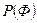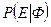m Решение. Применим теорему умножения вероятностей для нескольких событий. Вероятность того, что первой буквой будет «Ф», равна . Вероятность того, что второй буквой будет «Е», при условии, что букву «Ф» уже взяли, равна 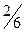и т.д. В итоге получаем:

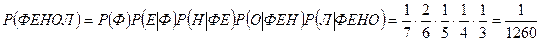.l

Пример 5. В урне 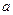белых и 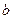черных шаров. Из урны вынимаются два шара. Найти вероятность того, что эти шары будут разных цветов.

m Решение. Рассмотрим события:

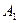— первый шар белый;

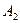— второй шар белый;

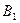— первый шар черный;

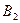— второй шар черный;

— шары разных цветов.

Очевидно, что 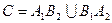, причем события 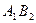и 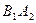несовместимы. По теореме сложения и по теореме умножения вероятностей для независимых событий:

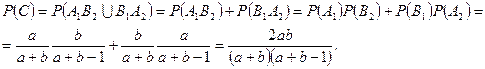
l

Пример 6. Техническая система состоит из n элементов, надежность каждого из них 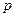. Выход из строя хотя бы одного влечет за собой выход всей системы. С целью повышения надежности системы производится дублирование, для чего выделено еще n таких же приборов. Определить, какой из способов дублирования надежнее:

§ дублирование каждого элемента (рис. 3.1);

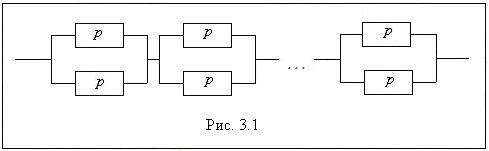
§ дублирование всей системы (рис. 3.2).

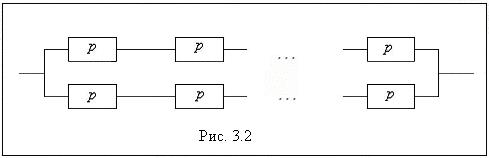
m Решение. Найдем надежность блока:

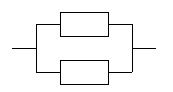
Для этого найдем вероятность выхода из строя. Блок выходит из строя, если выходит из строя каждый элемент, т.е. 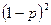. Тогда надежность блока равна 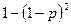. Далее система работает надежно, если работает каждый блок, т.о.:

.

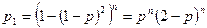Надежность системы

равна 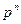. Отсюда надежность системы (рис. 3.2)

.

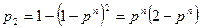Сравним 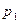и 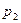, для этого нужно сравнить 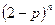и .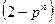

Докажем, что .

Подставим 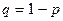, т.е.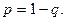

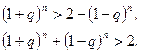
Далее достаточно раскрыть скобки.

Таким образом, надежнее дублирование каждого элемента. l

Date: 2015-06-07; view: 517; Нарушение авторских прав