
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет простейшей подвесной схемы трубопровода
|
|
Расчет подвесного трубопровода включает: расчет несущего троса, трубопровода, подвесок, пилонов и опор.
Несущий трос будем рассматривать как гибкую нить, загруженную распределенной нагрузкой д от веса троса и трубопровода, подвесок и различных элементов конструктивного оформления трубопровода. В соответствии с установивніейся в теории висячих систем терминологий нити могут быть с мальтми и большими стрелками прогиба. Практически все несущие тросы подвесных трубопроводов относятся к нитям с малыми проги-бами, критерием которых считается отношение стрелки прогиба ] к длине пролета Ь
: 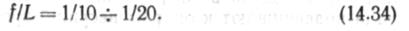
|
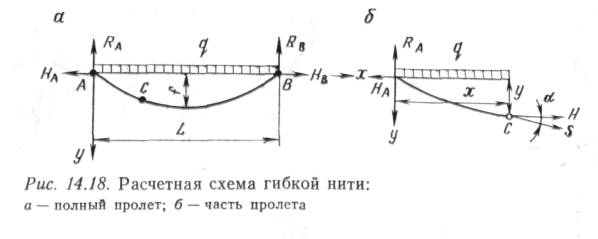
Статическая схема гибкой нити изображена на рис. 14.18. Проектируя силы на оси х, имеем: НА = НВ = Н.
Проекции сил на ось у дает условие КА + Кв = дІ*.
Сумма моментов сил относительно опоры В дает ЕМв — /?л^ = 0, откуда

Для определения натяжения нити необходимо знать величину Н, которую найдем из рассмотрения рапновесия части нити АС (см. рис. 14.18). Момент сил относительно точки С: МС = НУ. Отсюда

где Мс — момент сил такой же, как и для обычной балки. Его и называют балочным моментом.
Для показанных на рис. 14.18 сил І,Мв = дЬ2/2, откуда /?А = = 0,5<7^ и Мс = дх(1 — х)/2. Учитывая (14.36), ординату любого сечения найдем по формуле
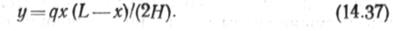

|
| Натяжение троса 5 найдем по формуле |
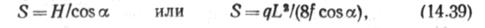
|
Принимая в (14.37) *=0,5^ и соответственно у=І, находим горизонтальную составляющую натяжения нити
где а —угол между Н и 5 (см. рис. 14.18, б). Из (14.39) видно, что наибольшее натяжение троса 5тах будет у опоры, а наи-меньшес при х=0,5І,. Величина
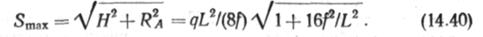
Подставив Н в (14.37), получим у = Цх(Ь — х)/Ь2.
Весьма важным является вопрос об изменении длины несущего троса. Дело в том, что по технологии строительства сначала подвешивают к опорам несущий трос, а затем к нему прикрепляют трубу. Поэтому трос от дополнительной нагрузки прогибается. Необходимо заранее знать, каков будет дополнительный прогиб.
Длину нити при начальной нагрузке у0 (вес троса и прикреп-ленных к нему оттяжек) определим из известной формулы
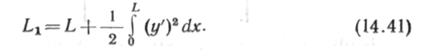

|
Используя (14.36) для <7о> находим (опуская в дальнейшем индекс С):
где Ро — поперечная сила в любом сечении.
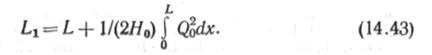
|
Подставляя (14.42) в (14.41), получаем
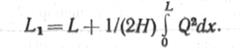
|
После загружения троса нагрузкой
Таким образом, для определения Ь\ необходимо найти интеграл \ 0?Лх.
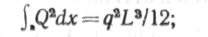
|
| для сосредоточенной силы, приложениой в сечениях х=Ь/2, |
По методу Верещагина (см. курс «Сопротивление матери-алов») для
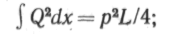
|
равномерно распределенной нагрузки
для равномерной нагрузки, приложенной от х—0 до *=0,5/-,
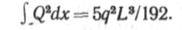
Формулы (14.35), (14.36), (14.39), (14.40), (14.43) полностью определяют как статические, так и геометрические характери-стики несущего троса, рассматриваемого как гибкая нить.
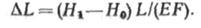
|
| Выполнив вычисления, получим |
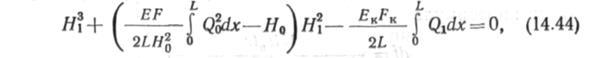
|
Отметим далее следующее. Величину Н\ после дополнительной загрузки троса от д0 до д найдем, учитывая, что
где Ек н Рк — модуль упругости и площадь сечения каната.
Это уравнение решается методом итераций или на ЭВМ.
Если нагрузка возрастает одновременно по всей длине Ь, то формула (14.44) может быть представлена в более простой форме:

Если необходимо учесть изменение температуры несущего каната, то в квадратную скобку (14.45) следует добавить член а.іЕкРк(і — /о), где аі — коэффициент линейного расширения; /о — температура при монтаже каната, / — температура в рассматриваемый момент времени.
Пример. К канату с модулем упругости ^„=1,5-10' Н/сы2, сечением ^„=20 см2 подвешены две трубы диаметром Ои=52,9 см с толщиной стенки 6 = 0,9 см. Расчетная нагрузка да складывается из веса единицы длины ка-ната и подвесок <7к=5,5 Н/см, двух незаполненных труб <7Тр=25,5 Н/см, пешеходного мостика <?и=10 Н/см, снега и льда <7сн=0,9 Н/см. Таким образом, <7<>=50 Н/см. После заполнения труб нефтью (^„=40 Н/см) общая нагрузка <7=90 Н/см. Пусть длина пролета /,= 1,5-10* см. В соответствии с (14.34) примем /0=0,1, і=1,5-103 см. По (14.38) Я0=0,93-10в Н. По (14.45), выполнив вычисления, получим /Л3+7,07-106 ЯІ2=2,278' 1017, от-куда //,= 1,62 -10е Н.
Соответствующий данному НІ прогиб /=1562 см. Таким образом, стрелка прогиба увеличилась на 62 см, а распор Н на 0,69- 10" Н.
Натяжение каната находим по (14,40) 5ШаІ=1,75- 10е Н.
По усилню -ѴщаІ проверяют несущую способность принятого каната. Для зтого определяют напряжения в канате ак=Ь'т»І/^к и сравнивают их с расчетным сопротивлением каната ак. р=0,4 авр. к, где авр. к — предел прочности проволок каната (временное сопротивление разрыву). Прочность каната будет обеспечена. если ак. р>ак. Расчет ветровых канатов и оттяжек
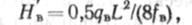
|
| а при ветре и темгіературном ІІерепаде |
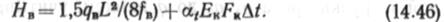
|
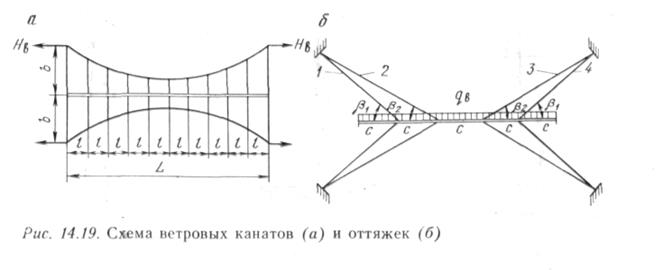
Размещение ветровых канатов и оттяжек изображено на рис. 14.19. Расчетная схема ветрового каната изображена на рис. 14.19,а. Основной нагрузкой для ветрового каната является ветровая нагрузка дв, приходящаяся на трубопровод. Для того чтобы ветровой канат сохранял необходимую расчетную форму, его предварительно (в период строительства) натягивают усилием, составляющим 0,5 усилия, создаваемого ветром.
Таким образом, в иериод безветрия усилие в канате
Величина Я„ по (14.46) несколько завышена по сравнению с действительной, которую можно определить по (14.38).
Дополнительный прогиб ветрового троса при этом можно найти по формуле
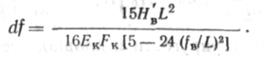
|
| Оттяжки (рис. 14.23, б) рассчитывают на ветровую нагрузку Ръ — ЦкС. При этом возникают силы |
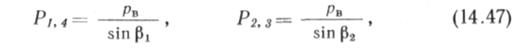
|
где /, 2, 3, 4 — номера оттяжек (см. рис. 14.19, б).
На ветровую нагрузку трубопровод проверяют, рассматривая его как балку на нескольких опорах (на рис. 14.19, а — шесть опор). Оттяжки, как и ветровые канаты, предварительно натягиваются на 50% от расчетных сил, определяемых по (14.47). Таким образом, в оттяжках нри ветре могут действовать силы, в 1,5 раза большие, чсм полученные по (14.47). Именно эти значения сил и должны приниматься в расчетных зависимостях при определении диаметра каната.
Date: 2015-06-07; view: 2869; Нарушение авторских прав