
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Балочные трубопроводы без компенсации удлинений
|
|
Схемы балочных трубопроводов без компенсации удлинений показаны на рис. 14.1. На рис. 14.1, а — многопролетный трубопровод неограниченной длины, на рис. 14.1,6, в, г — одно-, двух- и трехпролетные переходы. При числе пролетов более четырех трубопровод можно рассматривать как многопролетный. Расчетная схема однопролетного трубопровода изображена на рис. 14.2. Чтобы определить напряженное состояние многопролетного трубопровода, достаточно выяснить напряженное состояние одного пролета, ибо все пролеты находятся в одинаковых статических условиях. Напряженное состояние труб изменяется от начального, возникающего в незаполненном трубопроводе в период монтажа, до эксплуатационного. Можно указать на следующие основные моменты.
Трубопровод смонтирован и не заполнен продуктом. В этот период его температура равна t0, а интенсивность вертикальной распределенной нагрузки q0 соответствует весу единицы длины пустого изолированного трубопровода.
Трубопровод заполнен продуктом, давление которого р = 0. Температура продукта, а значит, и труб может быть t = to, t> ><0, t<_tn. Интенсивность вертикальной распределенной нагрузки в период эксплуатации увеличивается на дп, т. е. на вес продукта:
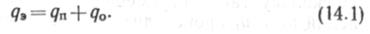
|
Трубопровод находится в эксплуатации. Температура t^O или t<0, а давление р = /?раб-
Дифференциальное уравнение упругой оси трубопровода представим в обычной форме: EIylv= — q.

где Е — модуль упругости; / — осевой момент инерции. Эта формула позволяет определить как напряжения, так и деформации в любом сечении пролета /.
Изгибающие моменты в опорных сечениях и прогиб в сечении х = //2 для начального состояния (q = q0):
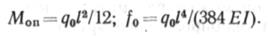
При заполнении трубопровода перекачиваемым продуктом, как правило, изменяются q, t и внутреннее давление р. За счет внутреннего давления в стенке труб возникают продольные напряжения апр=цс1кц, где акц — кольцевые напряжения; \i — коэффициент Пуассона, для пластичной стали ц, = 0,3. Они вызовут удлинение пролета / на величину
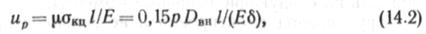
где б — толщина стенки труб.
За счет температурного перепада Д/, если бы трубопровод мог перемещаться в опорных сечениях Л и В в направлении оси х, участок / удлинился бы на величину
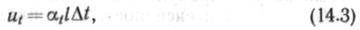
где at — коэффициент линейного расширения материала труб. Поскольку такое перемещение невозможно, компенсация удлинений ир и ut происходит за счет прогиба трубы в вертикальной плоскости. Этот прогиб fp,t, q найдем, имея в виду, что
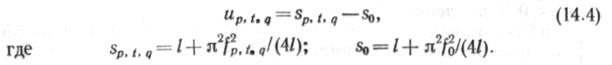
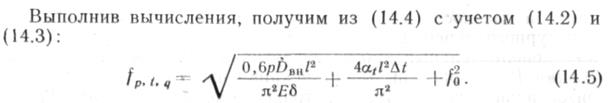
Продольную силу, которая возникает при этом в трубопроводе, можно найти, учитывая условие превращения потенциальной энергии внешних сил (q и Р) в потенциальную энергию упругого изгиба. Выполнив вычисления, находим
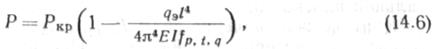
где Ркр = 4л2£///2— эйлерова критическая сила.
Значения fp,t,4 и Р получены без учета сжатия материала труб. На самом же деле под действием Р трубы сжимаются и прогиб будет меньше, чем полученный по (14.5), и соответственно будет отличаться от значения, вычисленного по (14.6). Учитывая сжатие труб в пролете /, находим
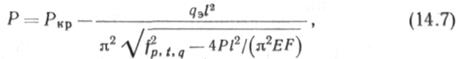
гДе /р, (, д принимается по (14.5), a <fo по (14.1).
Вычислив по (14.7) Р, можно определить соответствующий ему прогиб:
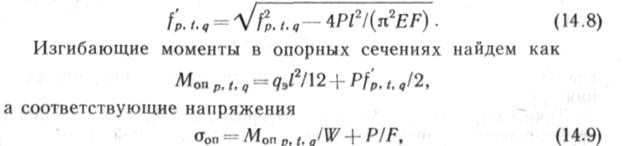
где W —момент сопротивления сечения труб; F — площадь сечения металла труб.
Рассчитывая надземный трубопровод указанным способом, можно обеспечить до определенного перепада температур Д/ устойчивую работу конструкции без компенсаторов за счет прогибов в вертикальной плоскости. Необходимо отметить, что компенсирующая способность прямолинейных балочных трубопроводов в проведенных нами опытах оказалась еще большей, так как трубопровод искривляется не только в вертикальной, но и в горизонтальной плоскостях, что создает дополнительный запас компенсационной способности. Причем искривление трубопровода между смежными опорами происходит не сразу, а при увеличении температуры до некоторого значения, после чего практически прекращается изгиб трубопровода в вертикальной плоскости, и дальнейшая компенсация температурных удлинений происходит за счет искривления трубопровода в горизонтальной плоскости. Это говорит о том, что до некоторого тем-пературного перепада А^ продольное усилие Р, обусловливающее дополнительный прогиб в вертикальной плоскости, меньше усилия РГ) которое вызывает искривление трубопроводов в горизонтальной плоскости. Как только продольное усилие Рв, необходимое для искривления трубопровода в вертикальной плоскости, станет больше усилия Рг, прямолинейная равновесная форма трубопровода в горизонтальной плоскости станет неустойчивой и произойдет искривление трубопровода в горизон-тальной плоскости.
Критическое значение силы Рг. кр установим, используя энергетический критерий устойчивости. Первая вариация от полной энергии Э деформации и изменения потенциала внешней нагрузки при незначительных отклонениях от равновесного положения должна быть 6.9 = 0.
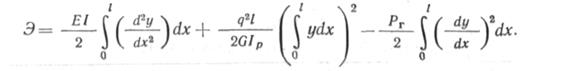
|
| Взяв первую производную от Э и приравняв ее нулю, найдем критическую силу |
Наши опыты показали, что форму искривления трубопровода в горизонтальной шюскости можно аппроксимировать в виде у=}&іпл,х/1. Тогда полную энергию трубопровода можно представить как

|
где 0 — модуль сдвига; ІР — полярный момент инерции сечения труб.
Таким образом, до Д/в, при котором РВ^РГ. кр, искривление трубопровода происходит только в вертикальной плоскости, а при Рг. кр<Рв в горизонтальной.
Для определения изменения продольной силы при измене-нии горизонтальной стрелки прогиба можно использовать точное дифференциалыюе уравнение упругой линии трубопровода. Однако, учитывая, что при незначительных стрелках прогиба продольная сила мало отличается от Рг. Кр, можно получить более простое решение.
Из выражения (14.5), в котором /0 = 0, а также условия Д/ = РГ кр[/(ЕР) находим действительный прогиб
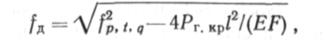
где /Р>«, д определяли по (14.5) при /0 = 0 и Д/ = / — І0 — Д^в.
Порядок расчета надземного многопролетного трубопровода следующий:
определяют при известных давлении, диаметре и прочностных характеристиках труб авр и сгт толщину стенки б;
с учетом найденной толщины стенки определяют расчетные нагрузки <7о и </;

|
находят длину пролета / из условия
| принимая М — 0,9атѴ7, где от — предел текучести; №—момент сопротивления сечения трубы. Из (14.9, 14.10) |

|
далее проверяют найденное / из условия обеспечения прочности трубопровода при заданных внутреннем давлении р и расчетном температурном перепаде А^; по (14.7) находят Р, а затем ГР,І,Я по (14.8);
по (14.9) находят аоп и сравнивают его с допускаемым значением напряжений; в СНиП 2.05.06—85 в качестве допускаемого напряжения рекомендуется величина
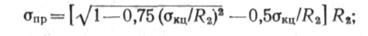
если сгоп^Япр, то пролет, рассчитанный по (14.11), выбран правильно.
Date: 2015-06-07; view: 1304; Нарушение авторских прав