Деформации срединной поверхности

Установим связь между перемещениями точек срединной поверхности и деформациями. Рассмотрим ненагруженную пластинку. Выберем произвольную точку a с координатами x, y (рис. 4.5). Возьмем две близкие точки b и c – с координатами ((х + dx); y) и
(x; (y + dy)) соответственно.

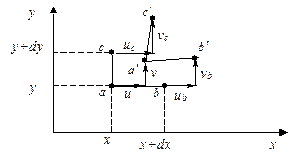
Рис. 4.5. Деформирование пластины

Под воздействием внешней нагрузки пластина деформируется, точки a, b, c перемещаются относительно системы координат и занимают положение, обозначенное точками a', b', c'. Проекции перемещения точки a являются функциями ее координат x, y: 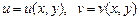. Координаты точек b, c отличаются от координат точки a на бесконечно малые величины dx и dy соответственно. Для вычисления перемещений в этих точках воспользуемся рядом Тейлора:

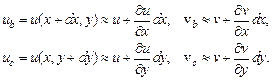(4.2)

На рис. 4.5 проекции перемещений точек a,b,c изображены стрелками. Для наглядности изменения длин отрезков и их углов поворота существенно увеличены. Относительные удлинения отрезка ab по направлению оси x и ac – по y определяются так: 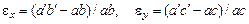. Из формул (4.2) следует оценка изменения длины отрезков dx и dy

.

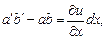
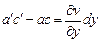Поэтому относительные удлинения выражаются через перемещения точек срединной поверхности по формулам:

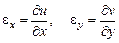. (4.3)

Деформация сдвига в окрестности выбранной точки a характеризует изменение углов между двумя направлениями ab и ac:

.

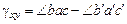Из рис. 4.5 следует, что сдвиг образован двумя слагаемыми: .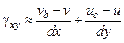

Из формул для перемещений (4.2) имеем:

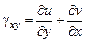. (4.4)

Date: 2015-06-07; view: 471; Нарушение авторских прав