
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Занятие 22-24. Решение задач элементарной геометрии методом геометрических преобразований
|
|
Задачи
1. На биссектрисе внешнего угла C треугольника ABC взята точка M. Доказать, что AC + CB < AM+MB.
2. На сторонах BC и CD квадрата ABCD взяты точки M и K соответственно, причем Ð BAM =Ð MAK. Доказать, что BM+KD=AK.
3. Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке O, причем 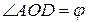 . Найти BC, если AB=a, CD=b, AD=c, AD > BC.
. Найти BC, если AB=a, CD=b, AD=c, AD > BC.
4. В выпуклом четырехугольнике ABCD Ð A =90°, Ð B =120°, AB=BC=a, 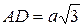 . Найти CD.
. Найти CD.
5. Диагонали параллелограмма ABCD пересекаются в точке O. На сторонах AB и CD вне параллелограмма построены правильные треугольники ABM и CDP; точки O 1 и O 2 – их центры. Точки O 3 и O 4 – центры окружностей, описанных около треугольников O 1 CD и O 2 AB. Докажем, что четырехугольник O 1 O 3 O 2 O 4 – параллелограмм, диагонали которого пересекаются в точке O.
6. Даны квадрат ABCD и точка M. Через точки A, B, C, D проведены прямые a 1, a 2, a 3, a 4, перпендикулярные прямым MD, MA MB и MC соответственно. Докажем, что прямые a 1, a 2, a 3, a 4, пересекаются в одной точке.
7. На сторонах AC и BC треугольника ABC построены вне треугольника квадраты AMHC и BPKC. Точки O 1 и O 2 – центры этих квадратов, а точка O – середина AB. Докажем, что отрезки OO 1 и OO 2 равны и перпендикулярны.
8. На сторонах AB и BC правильного треугольника ABC построены вне треугольника квадраты ABMN и BCPK. Точки B1 и С1 делят стороны AC и BA в отношении 2:1. Доказать, что отрезки MB1 и PC1 равны и пересекаются под углом 60°.
9. Доказать, что график функции 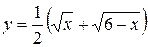 имеет ось симметрии, параллельную оси Oy.
имеет ось симметрии, параллельную оси Oy.
10. Доказать, что кривая 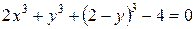 имеет ось симметрии, параллельную оси Ox.
имеет ось симметрии, параллельную оси Ox.
11. Доказать, что если противоположные стороны шестиугольника, описанного около окружности, параллельны, то они попарно равны.
12. Окружность пересекает две концентрические окружности: одну – в точках A и B, другую – в точках C и D,. Доказать, что хорды AB и CD параллельны и AC = BD, AD = BC.
13. Через центр квадрата проведены две взаимно перпендикулярные прямые. Доказать, что их точки пересечения со сторонами квадрата являются вершинами квадрата.
14. На сторонах правильного треугольника построены квадраты вне треугольника. Доказать, что их центры являются вершинами правильного треугольника.
3. Вариант контрольной работы по теме«Метод координат в пространстве»
Даны вершины 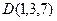 ,
, 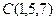 ,
, 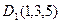 ,
, 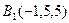 куба
куба 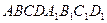 .
.
I. Найти: а) площадь треугольника 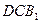 ; б) расстояние от точки
; б) расстояние от точки 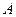 до прямой
до прямой 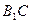 ; в) биссектрису
; в) биссектрису 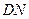 треугольника
треугольника 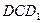 .
.
II. Найти: а) уравнение плоскости 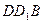 ; б) уравнение плоскости, содержащей грань
; б) уравнение плоскости, содержащей грань 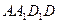 ; в) уравнение плоскости, проходящей через середину ребра
; в) уравнение плоскости, проходящей через середину ребра 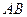 параллельно плоскости
параллельно плоскости 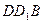 ; г) уравнение плоскости, касающейся в точке
; г) уравнение плоскости, касающейся в точке  сферы, описанной около куба.
сферы, описанной около куба.
III. Найти: а) длину перпендикуляра, проведенного из вершины 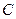 к плоскости
к плоскости 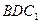 ; б) уравнения плоскостей, делящих пополам двугранные углы между плоскостями
; б) уравнения плоскостей, делящих пополам двугранные углы между плоскостями 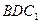 и
и 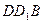 ; в) уравнения плоскостей, параллельных плоскости
; в) уравнения плоскостей, параллельных плоскости 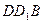 и отстоящих от нее на расстоянии 2.
и отстоящих от нее на расстоянии 2.
Установить расположение плоскости 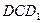 относительно сферы
относительно сферы 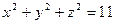 .
.
IV. Найти: а) общие и каноническое уравнения прямой пересечения плоскостей 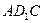 и
и 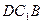 ; б) параметрические уравнения прямых
; б) параметрические уравнения прямых 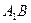 и
и 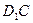 , и расстояние между этими прямыми; в) канонические уравнения прямых
, и расстояние между этими прямыми; в) канонические уравнения прямых 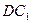 и
и 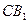 , и расстояние между этими прямыми.
, и расстояние между этими прямыми.
4. Вариант контрольной работы по теме
«Геометрические преобразования плоскости»
1. Даны преобразования
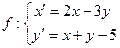 и
и 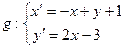 .
.
Найдите:
а) композицию преобразований 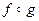 ;
;
б) формулы преобразования, обратного к f;
в) неподвижные точки и прямые преобразования g.
2. Напишите формулы аффинного преобразования плоскости, при котором точки 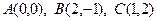 переходят соответственно в точки
переходят соответственно в точки 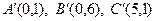 .
.
3. Напишите формулы:
а) центральной симметрии плоскости относительно точки 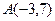 ;
;
б) параллельного переноса плоскости на вектор 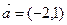 ;
;
в) поворота плоскости вокруг точки 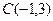 на угол
на угол 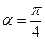 ;
;
г) осевой симметрии плоскости относительно прямой 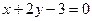 ;
;
д) гомотетии с центром в точке 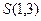 и коэффициентом
и коэффициентом 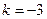 .
.
4. Определите вид преобразования плоскости, заданного формулами 
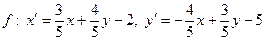 .
.
Вариант тестового задания для контроля остаточных знаний
1. Дан правильный шестиугольник 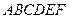 .
. 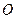 – точка пересечения его диагоналей. Сумма векторов
– точка пересечения его диагоналей. Сумма векторов 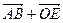 равна
равна
a) 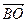 ; b)
; b) 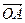 ; c)
; c) 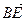 ; d)
; d) 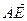 ; e)
; e) 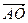 .
.
2. Векторное произведение векторов 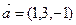 и
и  , координаты которых заданы относительно ортонормированного базиса, равно:
, координаты которых заданы относительно ортонормированного базиса, равно:
a) 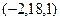 ; b)
; b) 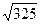 ; c)
; c) 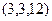 ; d)
; d) 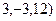 ; e)
; e) 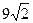 .
.
3. Заданы точки 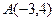 и
и 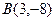 . Найдите координаты точки
. Найдите координаты точки 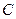 такой, что
такой, что 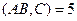 .
.
a) 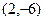 ; b)
; b) 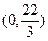 ; c)
; c) 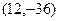 ; d)
; d) 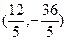 ; e)
; e) 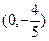 .
.
4. Общее уравнение прямой, проходящей через точку 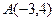 параллельно вектору
параллельно вектору 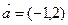 имеет вид
имеет вид
a) 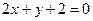 ; b)
; b) 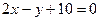 ; c)
; c) 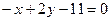 ;
;
d) 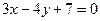 ; e)
; e) 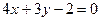 .
.
5. Относительно аффинной системы координат уравнение 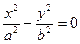 задает
задает
a) эллипс; b) гиперболу; c) параболу; d) мнимый эллипс; e) пару пересекающихся прямых.
6. В треугольнике 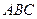
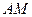 и
и 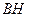 – медианы. Найдите координаты вектора
– медианы. Найдите координаты вектора 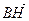 в базисе
в базисе  .
.
7. Составьте уравнения биссектрис углов, образованных при пересечении прямых 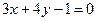 и
и 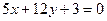 .
.
8. Составьте каноническое уравнение эллипса, если его малая ось равна 6, а расстояние между фокусами равно 8.
9. Вычислить координаты вершин ромба, если известны уравнения прямых, содержащих соответственно две его стороны и одну из его диагоналей: 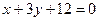 ,
, 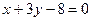 ,
, 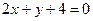 .
.
10. Составьте уравнение множества всех точек плоскости, расстояние от каждой из которых до точки 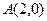 в два раза больше расстояния до прямой
в два раза больше расстояния до прямой 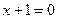 .
.
Литература
1. Аналитическая стереометрия: сост. Ю.Н. Мухин, В.П. Толстопятов, Г.Ф. Шульгина. – Свердловск: СГПИ, 1991. – 36 с.
2. Аргунов, Б. И. Преобразования плоскости: учеб. пособие для студ.-заочников / Б. И. Аргунов. – М.: Просвещение, 1976.
3. Атанасян, Л.С. Геометрия. Ч. 1: учеб. пособие /Л.С. Атанасян, В.Т. Базылев. – М.: Просвещение, 1986. – 336 с.
4. Атанасян, Л.С. Сборник задач по геометрии. Ч. 1 /Л.С. Атанасян, В.А. Атанасян. – М.: Просвещение, 1973. – 256 с.
5. Базылев, В.Т. Геометрия. Ч 1: учеб. пособие / В.Т. Базылев, К.И. Дуничев, В.П. Иваницкая. – Б.м.:Б.и., 2004. – 351 с.
6. Векторная алгебра и аналитическая геометрия в системе таблиц: сост. Т.А. Унегова. – Екатеринбург: УрГПУ, 1999. – 34 с.
7. Геометрические преобразования: сост. Ю. Н. Мухин, Т. А. Унегова, Г. Ф. Шульгина. – Екатеринбург: УрГПУ, 1996. – 32 с.
8. Дидактический материал по геометрии. / Методическая разработка; Сост. Т.А. Унегова, Г.Ф. Шульгина. – Екатеринбург: УрГПУ, 1986. – 35 с.
9. Ефимов, Н.В. Высшая геометрия: учеб. пособие / Н.В. Ефимов. – М.: Физматлит, 2003. – 584 с.
10. Жафяров, А.Ж. Геометрия. Ч.: учеб. пособие / А.Ж. Жафяров. – Новосибирск: Сибирское университет. изд-во, 2002. – 271 с.
11. Метод координат в пространстве. / Индивидуальные задания; Сост. В.П. Толстопятов, Т.А. Унегова, О.В. Хохлова. – Екатеринбург: УрГПУ, 2003. – 30 с.
12. Саранцев, Г. И. Сборник задач на геометрические преобразования / Г. И. Саранцев 2-ое изд. – М.: Просвещение, 1981.
Учебно-методическое издание
Геометрия.
Материалы для практических занятий.
I курс, 2 семестр
Составители:
Толстопятов В.П., к. ф.-м. н., доцент, профессор кафедры высшей математики
Дударева Н.В., к. пед. н., доцент, доцент кафедры высшей математики
Унегова Т.А., к. ф.-м. н., доцент, доцент кафедры высшей математики
ГЕОМЕТРИЯ
Материалы для практических занятий
I курс, 2 семестр
Подписано в печать Формат 60х84/16
Бумага для множительных аппаратов. Усл. печ. л. 2,5
Тираж экз. Заказ
Уральский государственный педагогический университет
620017 Екатеринбург, пр. Космонавтов, 26
Date: 2015-05-04; view: 1202; Нарушение авторских прав