Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Занятие 14. Отображения, их виды. Преобразования множества. Композиция преобразований
|
|
Задачи
1. Какие из приведенных ниже высказываний верны, а какие – нет?
а) Функция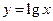 
есть отображение множества всех действительных чисел 
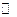в множество ;
б) Функция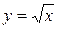 
есть отображение множества всех неотрицательных действительных чисел 
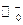во множество ;
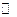в) Вычитание натуральных чисел есть отображение множества N × N во множество целых чисел.
2.. На плоскости задана аффинная система координат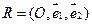 
. Каждой точке 
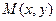ставится в соответствие точка 
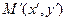, где 
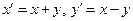. Тем самым задано отображение плоскости в себя. Найти образы и прообразы точек 
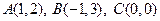. Сделать рисунок.
3. Рассматривая функцию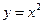 
как отображение множества R в себя, найти:
а) образ отрезка [0; 2];
б) полный прообраз отрезка [0; 1];
в) множество значений данного отображения.
4. Рассматривая функцию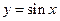 
как отображение множества R в себя, найти:
а) образ отрезка [0; π ];
б) полный прообраз числа 0;
в) множество значений данного отображения.
5. Пусть А={1; 2; 3; 4}, В={а; b; с; d; е}. Задать какое-нибудь отображение f: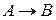 
, которое было бы инъективным, но не сюръективным.
6. Пусть A ={1; 2; 3; 4; 5}, В ={ а; b; с; d }. Задать какое-нибудь отображение f: 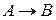, которое было бы сюръективным, но не инъективным.
7. Пусть A ={1; 2; 3; 4}, В ={ а; b; с; d }. Задать какое-нибудь отображение f: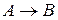 
, которое было бы инъекцией и сюръекцией, т.е. биекцией.
8. Рассматривая функцию y = sin x как отображение множества R в отрезок [–1; 1], выяснить, является ли это отображение инъекцией? сюръекцией? биекцией?
9. Рассматривая функцию y = sin x как отображение отрезка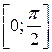 
в отрезок [–1; 1], выяснить, является ли это отображение инъекцией? сюръекцией? биекцией?
10. Рассматривая функцию y = sin x как отображение отрезка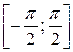 
в отрезок [–1; 1], выяснить, является ли это отображение инъекцией? сюръекцией? биекцией?
11. Доказать, что если отображение f: 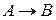является биекцией, то всякий элемент множества B имеет ровно один прообраз.
12. Дано отображение f: 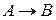. Доказать, что если всякий элемент множества B имеет ровно один прообраз, то f – биекция (признак биективности).
13. Задать какое-нибудь преобразование:
а) множества A ={1; 2; 3};
б) множества B ={ а; b; с; d }.
14. Отображение f плоскости в себя в некотором аффинном репере задано формулами x′ = x + y +1, y′ = x – y +2. Доказать, что f – преобразование плоскости.
15. Отображение f плоскости в себя в некотором аффинном репере задано формулами x′ = а 1 x + b 1 y + c 1, y′ = а 2 x + b 2 y + c 2 (1). Доказать, что отображение f является преобразованием тогда и только тогда, когда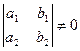 
.
16. Являются ли преобразованиями плоскости, отображения, заданные следующими формулами:
а) x′ = x – 2 y + 5, y′ = 3 x – 6 y + 1;
б) x′ = x – 2 y + 5, y′ = 3 x – 5 y + 1;
в) x′ = x + 1, y′ = x + y.
Date: 2015-05-04; view: 874; Нарушение авторских прав