Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Занятие 15. Параллельный перенос и поворот плоскости
|
|
Задачи
1. При переносе на вектор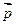 
точка 
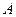переходит в точку 
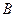, а при переносе на вектор 
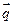точка 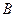переходит в точку 
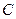. Найти: а) образ точки 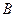при переносе на вектор 
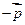; б) образ точки 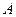при переносе на вектор 
.
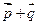2. Длины отрезков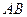 
и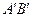 
равны. Отображение 
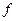плоскости переводит данную точку 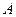в точку 
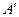и точку 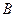в точку 
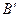. Является ли отображение 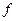параллельным переносом?
3. Сколько существует параллельных переносов плоскости, отображающих прямую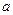 
на параллельную ей прямую 
?
4. Доказать, что параллельный перенос является преобразованием плоскости.
5. Составить формулы параллельного переноса на вектор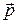 
, если известно, что при этом переносе точка A (1; 2) переходит в точку А 1, принадлежащую прямо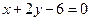й 
и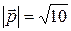 
.
6. Относительно группы параллельных переносов являются эквивалентными следующие фигуры:
1) две окружности одного и того же радиуса; 2) два направленных отрезка одинаковой длины и одного направления; 3) сонаправленные лучи; 4) два квадрата с равными сторонами?
7. Дан параллелограмм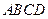 
; 
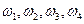– окружности радиуса R с центрами в точках 
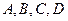соответственно. Найти:
1) образы окружносте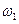й 
и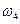 
при переносе на вектор 
;
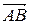2) образы окружностей 
и 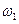при переносе на вектор 
;
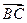3) образ прямой, проходящей через точку 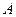и перпендикулярной прямой 
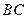, при переносе на вектор 
.
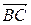8. Дан правильный треугольник 
(буквы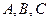 
расставлены в порядке обхода вершин по часовой стрелке); точка 
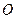– центр треугольника. Укажите: а) образ точки 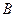при повороте 
;
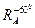б) образ точки B при повороте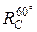 
;
в) образы точек A, B, C при повороте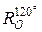 
;
г) образы точек A, B, C при повороте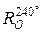 
.
9. Сколько существует различных поворотов, переводящих точку 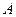в точку ?
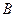10. Дан квадрат ABCD с центром O. Найти образы следующих фигур при повороте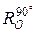 
:
а) луч AB;
б) прямая, проходящая через точку B и параллельная прямой AC;
в) полуплоскость, определяемая прямой BC и содержащая точку O.
11. Дан правильный треугольник ABC с центром O. Найти образы следующих фигур при повороте :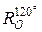
а) отрезок BC;
б) луч CA;
в) полуплоскость, определяемая прямой AB и не содержащая точку O.
12. При повороте 
точка 
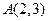переходит в точку 
. Составить формулы поворота, если известно, что его центр принадлежит прямой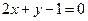 
. Найти образ начала координат при этом повороте.
13. При центральной симметрии ZА точка М переходит в точку K, а при центральной симметрии ZВ точка K переходит в точку P. Доказать, что при переносе на вектор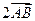 
точка M переходит в точку P.
14. Доказать, что всякое преобразование плоскости, заданное в аффинном репере формулами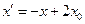 
, 
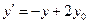, является центральной симметрией с центром в точке S (x 0; y 0).
15. На прямой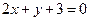 
найти точку, которая при центральной симметрии с центром в начале координат переходит в точку, принадлежащую прямой 
.
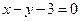16. Составить формулы центральной симметрии ZS, при которой точка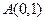 
переходит в точку, принадлежащую прямой 
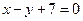, если известно, что центр S принадлежит прямой 
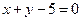x+y –5=0.
17. Относительно группы поворотов с общим центром следующие фигуры являются эквивалентными:
1) две гиперболы с центром в точке ; 2) два луча с началом в точке 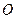; 3) две произвольные прямые; 4) две прямые, одинаково удаленные от точки ?
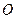Date: 2015-05-04; view: 1153; Нарушение авторских прав