Занятие 19. Геометрические свойства аффинных преобразований

Задачи

1. Преобразование плоскости задано в аффинном репере формулами 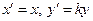, где k ≠0. Доказать, что данное преобразование является аффинным.

2. Аффинное преобразование f задано в ортонормированном репере формулами x′ = x, y′ = ky, где k ≠0. Доказать, что если 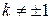, то преобразование f не является подобием (и, следовательно, не является движением).

3. Даны треугольники ABC и A′B′C′. Аффинное преобразование f задано тремя парами соответствующих точек: , , 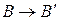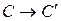. Построить образ произвольной точки M.

4. Перспективно-аффинное преобразование задано осью s и парой соответствующих точек A и A′, причем прямые AA′ и s пересекаются. Построить образ заданной точки.

5. Доказать, что не существует такого аффинного преобразования, при котором: , , ;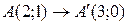

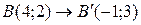6. Косое сжатие задано осью и парой соответствующих точек M и M′. Построить образ данного треугольника ABC.

7. Сдвиг задан осью и парой соответствующих точек M и M′. Построить образ данного треугольника ABC.

8. Верны ли утверждения

· Чтобы доказать, что отрезок AB параллелен прямой b и делится прямой a в отношении m: n, достаточно установить, что точка A переходит в точку B при косом сжатии, заданном осью a, направлением b и коэффициентом, равным .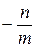

· Чтобы доказать, что точка пересечения прямых a и b принадлежит прямой c, достаточно установить, что при некотором косом сжатии или сдвиге с осью c прямая a отображается на прямую b?

9. Доказать, что в любой трапеции точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

10. На сторонах CA и CB треугольника ABC взяты, соответственно, точки M и N так, что 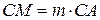, 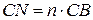. Медиана CD пересекает отрезок MN в точке P. Найти отношение MP: PN.

Date: 2015-05-04; view: 838; Нарушение авторских прав