Занятие 16. Осевая и скользящая симметрия

Задачи

1. Отрезк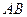и и 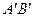являются диагоналями квадрата 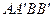. Отображение 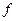плоскости переводит точку 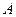в точку 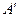и точку 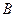в точку 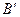. Отображение 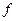может быть

1) поворотом; 2) осевой симметрией; 3) композицией двух осевых симметрий; 4) параллельным переносом?

2. Точка M лежит внутри прямого угла AOB. При осевой симметрии S_OA точка M переходит в точку P, а при осевой симметрии S_OB точка P переходит в точку K. Доказать, что при центральной симметрии Z_O точка M переходит в точку K.

3. Дан ромб ABCD. Найти образ полуплоскости, определяемой прямой AB и не содержащей точку C, при осевой симметрии с осью AC.

4. Прямая a содержит высоту AO, проведенную к основанию BC равнобедренного треугольника ABC. На стороне AB взяты точки M и P так, что AM = MP = PB, а на стороне AC – точки N и K так, что AN = NK = KC. Найти образы отрезка BN и луча MK при осевой симметрии S_a.

5. При осевой симметрии, осью которой является прямая 2 x – y =0, точка A оси Ox переходит в точку B, принадлежащую прямой 3 x + y +1=0. Найти точки A и B.

6. При каком взаимном расположении прямых 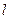и 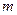справедливо равенство ?

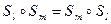7. Составить формулы осевой симметрии, при которой точка M (2; 5) переходит в точку М′ (0; 1).

8. Доказать, что если при скользящей симметрии 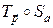точка M переходит в точку М′, то середина отрезка MМ′ принадлежит оси a.

9. Составить формулы скользящей симметрии 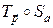, если 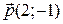, а ось a задана уравнением x +2 y –1=0.

1. Найти ось скользящей симметрии 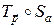, при которой точка M (1;5) переходит в точку М′ (5; 3), а .
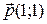2. Найти ось a и вектор 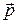скользящей симметрии 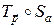, при которой точка A (1; 2) переходит в точку B (–1; 0), а точка B переходит в точку C (1; –2). Составить формулы этой скользящей симметрии.
3. Доказать, что если 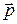|| a, то .

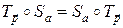Date: 2015-05-04; view: 1065; Нарушение авторских прав