Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Магнитное поле тороида
|
|
Тороид – тонкий провод, плотно намотанный на каркас в форме тора (круга, бублика).
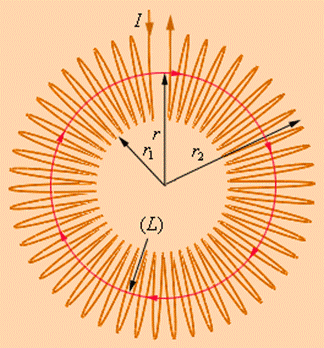Возьмём контур в виде окружности радиуса ri, центр которого совпадает с центром тора, радиуса r (r1 < ri < r2). В силу симметрии вектор B в каждой точке направлен по касательной к контуру. Следовательно,
Это длина контура, окружность.
Если контур проходит внутри тороида, то он охватывает ток 2p×r×n×I (n – число витков на единицу длины). Тогда по теореме о циркуляции вектора B получаем.
Откуда получаем.
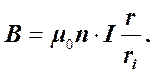А для напряжённости имеем. 
Если внутри тороида имеется сердечник, то выражение для индукции магнитного поля примет вид.
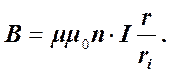
Контур вне тороида токов не охватывает, поэтому B = 0 (B ×2p×r = 0).
Для тороида, где r много больше радиуса витка, отношение r/ri» 1, т.е. r» ri. Для такого тора индукция и напряжённость будут равны.
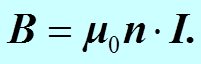
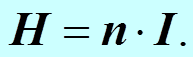
В тороиде индукция магнитного поля однородна по величине, т.е. по модулю, но его направление в каждой точке различно.
Date: 2015-05-04; view: 1000; Нарушение авторских прав