Магнитное поле соленоида. Используем теорему о циркуляции для расчета магнитного поля соленоида

Используем теорему о циркуляции для расчета магнитного поля соленоида. Соленоид – это проводник, намотанный по винтовой линии на поверхность цилиндрического каркаса. Пусть длинный соленоид с током 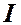имеет 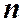витков на единицу длины. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно заменить замкнутым витком. На рисунке показаны линии магнитной индукции вне и внутри соленоида. Опыт показывает, что чем длиннее соленоид, тем меньше поле вне него. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено внутри его, а поле снаружи отсутствует. Линии вектора 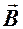внутри соленоида направлены по оси так, что образуют с направлением тока в соленоиде правовинтовую систему.

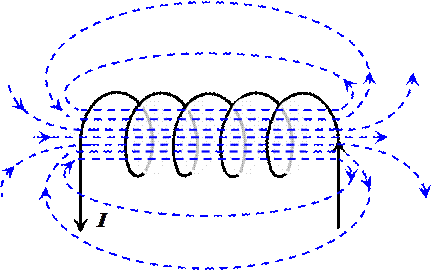Для расчета поля внутри длинного соленоида выберем прямоугольный контур АВСДА так, как это показано на нижнем рисунке.

Циркуляцию вектора 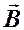по замкнутому контуру АВСДА, который охватывает витков, вычислим по формуле:

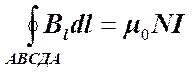
Интеграл по АВСДА можно представить в виде четырех интегралов: по АВ, ВС, СД и ДА. На участках АВ и СД контур перпендикулярен линиям магнитной индукции и 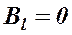. На участке ДА контур совпадает с линией магнитной индукции и циркуляция вектор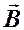а равна 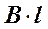. На участке ВС вне соленоида 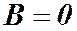. В итоге получаем:

Итог: , отсюда 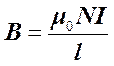. Поскольку 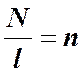, то окончательно получим .

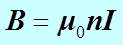Таким образом, поле внутри соленоида однородно (края соленоида не рассматриваем). Произведение 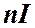называется числом ампервитков соленоида и относится к его характеристикам.

При выводе формулы для магнитного поля соленоида мы допустили некорректность: мы приняли интеграл по внешней части контура равным нулю, несмотря на то, что линии магнитного поля замкнуты и, строго говоря, внешнее поле не равно нулю. Однако это некорректность принципиально на результате не отражается.

Date: 2015-05-04; view: 1545; Нарушение авторских прав