
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Движение заряженной частицы в однородном магнитном поле
|
|
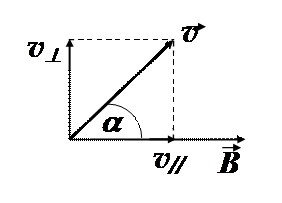 Пусть заряд q влетает в однородное магнитное поле, индукция которого равна B, со скоростью v, направленной под углом a к направлению вектора магнитной индукции. Под действием силы Лоренца заряд приобретает постоянное по величине нормальное ускорение.
Пусть заряд q влетает в однородное магнитное поле, индукция которого равна B, со скоростью v, направленной под углом a к направлению вектора магнитной индукции. Под действием силы Лоренца заряд приобретает постоянное по величине нормальное ускорение.
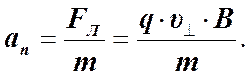
 a - угол между векторами скорости и магнитной индукции.
a - угол между векторами скорости и магнитной индукции.
Если скорость изменяется только по направлению, т.е. движение с постоянным по величине нормальным ускорением, есть движение по окружности, радиус которой определяется следующим выражением.
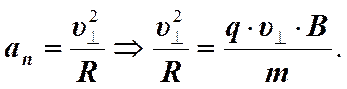 Отсюда радиус будет равен.
Отсюда радиус будет равен.
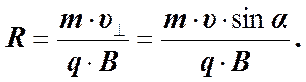 (1)
(1)
Отношение заряда к массе (q/m) называется удельным зарядом.
Найдём время одного оборота (период) T. Для этого нужно разделить длину окружности 2pR на v^ (скорость вращения заряда).


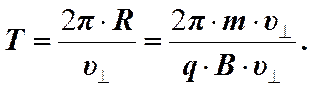
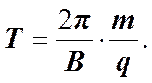 Период вращения заряженной частицы оказывается не зависящим от скорости. Собственная круговая частота (число оборотов за 2p секунд) равна.
Период вращения заряженной частицы оказывается не зависящим от скорости. Собственная круговая частота (число оборотов за 2p секунд) равна.
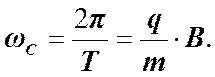
Составляющая силы Лоренца в направлении вектора магнитной индукции (или в направлении v||) равна нулю. Поэтому повлиять на величину скорости v|| сила Лоренца не может.
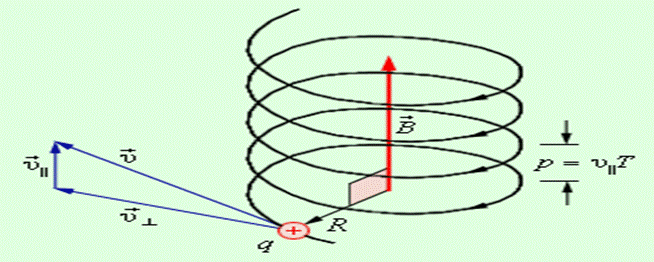
Движение заряженной частицы в магнитном поле можно представить как наложение двух движений: 1) перемещение вдоль вектора B со скоростью v|| = v×cosa; и 2) равномерное вращение в плоскости перпендикулярной вектору B. Радиус окружности, по которой происходит вращение, определяется формулой (1). Траектория движения – спираль, ось которой совпадает по направлению с направлением вектора B. Шаг спирали будет определяться выражением.
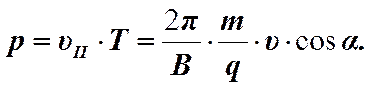
Date: 2015-05-04; view: 1140; Нарушение авторских прав