Циркуляция вектора магнитной индукции

Возьмём контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора , т.е.

Рассмотрим вначале случай, когда контур лежит в плоскости, перпендикулярной току (ток направлен за чертёж). В каждой точке поля вектор направлен по касательной к окружности, проходящей через эту точку (линии индукции прямого тока окружности). Воспользуемся свойством скалярного произведения векторов , где dl_B – проекция вектора dl на направление вектора индукции B.

R – расстояние от тока до вектора dl. Мы знаем, что для прямого тока индукция равна.

Тогда получим.

Отсюда найдём циркуляцию вектора магнитной индукции.

При обходе контура угол a изменяется от нуля до 2p, при этом радиальная прямая поворачивается в одном направлении. Для напряжённости магнитного поля выражение для циркуляции будет иметь вид.

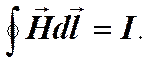
По-другому обстоит дело, если ток не охватывается контуром. В этом случае при обходе контура радиальная прямая поворачивается сначала в одном направлении (1 ®2),

а потом в другом (2 ® 1).

В этом случае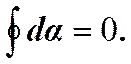

Итак, в общем случае (1)

I – ток, охватываемый контуром.

Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

Если контур охватывает несколько токов, то выражение (1) примет вид.

(2)

Или для напряжённости магнитного поля.

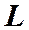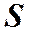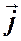Если ток распределен по объему, где расположен контур , то этот ток можно представить, как . Интеграл берется по произвольной поверхности , "натянутой" на контур . Плотность тока под интегралом – это плотность в точке, где расположена площадка . Вектор образует с направлением обхода по контуру правовинтовую систему.

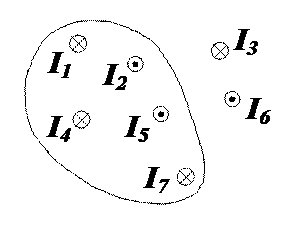Таким образом, уравнение для циркуляции в общем случае будет выглядеть так:

Date: 2015-05-04; view: 748; Нарушение авторских прав