Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Магнитное поле на оси кругового тока
|
|
 |
Пусть электрический ток силой
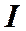течет по проводнику радиусом 
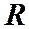. Найдем магнитное поле на оси 
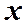тока в точке А, находящейся на расстоянии 
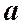от центра. Разобьем круговой ток на элементы тока длиной 
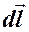и проведем от произвольного элемента тока радиус-вектор 
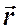в точку А. Поскольку все элементы тока 
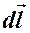перпендикулярны 
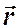и удалены от А на одинаковое расстояние, то модуль вектора магнитной индукции, создаваемой в этой точке произвольным элементом тока, определяется следующим выражением:
.
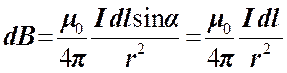
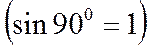Вектор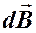 
направлен перпендикулярно плоскости, в которой располагаются вектора 
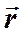и 
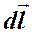, как показано на рисунке.
Разложим вектор 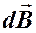на две составляющие: параллельную оси 
– 
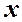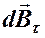и перпендикулярную ей – 
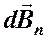. Очевидно, что составляющие 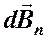, созданные элементами тока, располагающимися на противоположных концах любого диаметра кругового проводника, равны по величине и противоположны по направлению. Следовательно, эти составляющие уничтожают друг друга. В итоге результирующая величина вектора магнитной индукции не содержит нормальной составляющей и направлена вдоль оси кругового тока. Поэтому вектор магнитной индукции можно определить, просуммировав составляющие модулей вектора 
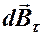(учитывая то, что этот вектор направлен вдоль положительной нормали к контуру с током):
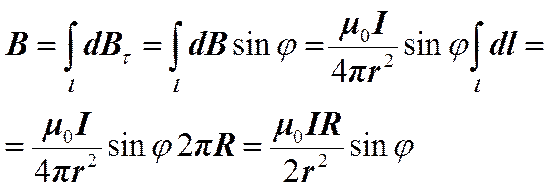
Преобразуем полученное выражение, учитывая, что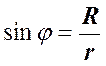 
, 
.
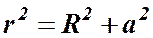После подстановки получим
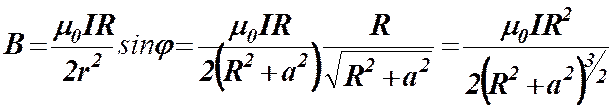
В центре кругового тока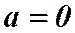 
, индукция магнитного поля равна
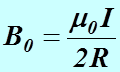(7)
Вдали от контура на оси (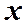
):
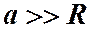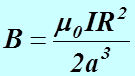(8)
Если умножить числитель и знаменатель этого выражения на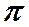 
, получим:
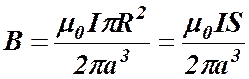
где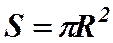 
– площадь, охватываемая круговым током.
Учитывая, что произведение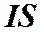 
для контура с током есть магнитный момент контура, введенный нами ранее, выражение для индукции магнитного поля, созданного замкнутым круговым током вдали от тока, можно записать в виде:
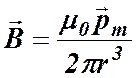(9)
Записывая это соотношение, приняли, что вдали от кругового тока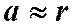 
.
 |
Графическими методами покажем вид магнитного поля. На рисунке изображены линии магнитной индукции поля кругового тока. Показаны линии, лежащие в одной из плоскостей, проходящей через ось тока и показаны направления векторов индукции магнитного поля, образованного круговым током. Векторы индукции показаны в точке, лежащей на оси, которая проходит через центр кругового тока, как это изображено на рисунке. Векторы образуют симметричный конический веер. Из соображений симметрии следует, что результирующий вектор
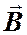направлен вдоль оси контура.
Date: 2015-05-04; view: 1509; Нарушение авторских прав