
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розв'язання. Кількість бітів, необхідна для кодування 8 повідомлень різними комбінаціями двійкового коду, визначається з нерівності
|
|
Кількість бітів, необхідна для кодування 8 повідомлень різними комбінаціями двійкового коду, визначається з нерівності
N £ 2k,
де N – об'єм алфавіту джерела повідомлень; k – довжина кодової комбінації у бітах.
Звідки випливає, що k³ log2 N.
У даному випадку для кодування N =8 повідомлень необхідна кількість бітів k ³ 3.
Довжина кодових слів при кодуванні лінійним блоковим кодом інформаційних повідомлень довжиною k символів n= k+r, де r – кількість перевірних символів, що додаються до інформаційного повідомлення для забезпечення можливості виявлення і/або виправлення помилок, що виникають при передачі по каналу зв'язку із завадами.
Знайдемо кількість перевірних розрядів r, необхідну для виправлення помилок кратності l = 1.
Для того щоб лінійний блоковий код міг виправляти помилки кратності не більшої l, необхідно і достатньо, щоб найменша кодова відстань між його словами dmin відповідала нерівності
dmin ≥ 2 l+ 1.
У даному випадку для виправлення помилок ваги l= 1 мінімальна кодова відстань dmin ³ 3.
Мінімальну кількість перевірних розрядів r визначаємо, скориставшись формулою нижньої границі Плоткина:
r³ 2 dmin - 2 – log2 dmin.
У даному випадку необхідна кількість перевірних елементів r = ù 2×3 – 2 – log2 3 é» ù 4 – 1,585 é= 3.
Тоді довжина кодового слова n= k+r = 3+3= 6.
Твірна матриця лінійного блокового коду складається із двох частин: інформаційної Ik×k (одиничної підматриці) і перевірної Рk ´ r. Перевірна підматриця Pk ´ (n-k) будується підбором r -розрядних комбінацій з кількістю одиниць у рядку ≥ dmin - 1 і кодовою відстанню між рядками ≥dmin - 2. При цьомусі рядки твірної матриці лінійно незалежні, вага кожного кодового слова, що входить у твірну матрицю, і кодова відстань між ними ≥ dmin.
Наведемо можливий варіант твірної матриці лінійного блокового (3,6)-коду:

 .
.
Ik×k Pk ´ (n-k)
Перевірна матриця заданого коду складається із транспонованої перевірної частини твірної матриці P(n-k ) ×k і одиничної підматриці I(n-k) × ( n-k):
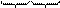
 .
.
P T (n-k)´-k I T k×k
Виходячи з твірної матриці, будуємо таблицю всіх можливих кодових слів заданого коду:
(m 1, m 2, m 3)® (u 1, u 2, u 3, u 4, u 5, u 6)= =(m 1, m 2, m 3, r 1, r 2, r 3),
де кодове слово u = m´G(k, n).
1) (000)® (000000); 2) (001)® (001110);
3) (010)® (010011); 4) (011)® (011101);
5) (100)® (100101); 6) (101)® (101011);
7) (110)® (110000); 8) (111)® (111001).
Неважко переконатися, що мінімальна кодова відстань отриманого коду dmin =3.
Іншим способом таблицю кодів можна побудувати, розглянувши всі можливі лінійні комбінації (порозрядні суми за модулем 2) кодових слів, що входять у твірну матрицю коду.
Припустимо передається повідомлення m =(101).
Кодовим словом на виході кодера буде послідовність
u = m ´ G = (101)´  = (101011).Нехай при передачі цього кодового слова по каналу зв'язку із завадами в ньому виникла помилка. Наприклад, прийнята послідовність y =(101111).
= (101011).Нехай при передачі цього кодового слова по каналу зв'язку із завадами в ньому виникла помилка. Наприклад, прийнята послідовність y =(101111).
Для декодування прийнятої послідовності на прийомній стороні обчислюється кодовий синдром
S = y´H T,
де y – прийнята кодована послідовність; H T - транспонована перевірна матриця.
Обчислимо синдром прийнятого вектора y:
S = (101111) ´ 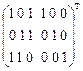 = (100) ¹ 0 - значення синдрому збігається із 4 -м стовпцем перевірної матриці H, отже, помилка виникла в 4 - му розряді.
= (100) ¹ 0 - значення синдрому збігається із 4 -м стовпцем перевірної матриці H, отже, помилка виникла в 4 - му розряді.
Виправляємо помилку і декодуємо кодове слово так:
(101111) ® (101011) ® (101).
Задачі до розділу 10
1 Перевірна матриця лінійного блокового (3, 6)- коду має вигляд
 .
.
Побудувати твірну матрицю і систему перевірних рівнянь коду. Визначити синдром виправлення однократних помилок в комбінаціях коду. Навести приклад виявлення і виправлення помилки кодом.
2 Перевірна матриця лінійного блокового (3, 6)- коду має вигляд
 .
.
Побудувати твірну матрицю коду. Закодувати повідомлення 101, 001. Використовуючи синдром, визначити помилку (якщо вона є) і декодувати послідовності 011001; 110100; 001111.
3 Лінійний блоковий код заданий твірною матрицею вигляду
 .
.
Побудувати перевірну матрицю коду. Визначити синдром виправлення поодиноких помилок цим кодом. Побудувати таблицю кодів. Навести приклад виявлення і виправлення помилки кодом.
4 Перевірна матриця коду має вигляд
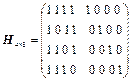 .
.
Побудувати твірну матрицю коду. Визначити мінімальну кодову відстань Хеммінга і можливості коду виявляти і виправляти помилки. Визначити синдром виправлення поодиноких помилок кодом. Навести приклад виявлення і виправлення помилки.
5 Твірна матриця лінійного блокового коду має вигляд
 .
.
Побудувати перевірну матрицю коду. Визначити синдром виправлення поодиноких помилок кодом і його можливості виявляти і виправляти помилки. Навести приклад виправлення помилки.
6 Твірна матриця лінійного блокового (4, 7)- коду має вигляд
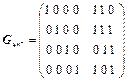 .
.
Побудувати перевірну матрицю коду й закодувати комбінації 0010, 1010, 1110. Визначити синдром виправлення поодиноких помилок в комбінаціях заданого коду. Навести приклад виправлення помилки. Скільки помилок можна виявити/ виправити цим кодом?
7 Перевірна матриця лінійного блокового (4, 7)- коду має вигляд
 .
.
Побудувати твірну матрицю коду. Закодувати комбінації 0010, 1010, 1110. Визначити синдром виправлення поодиноких помилок в комбінаціях заданого коду. Виправити помилку і декодувати послідовності 1010101, 0010101. Визначити можливості коду виявляти і виправляти помилки.
8 Перевірна матриця лінійного блокового (4, 7)- коду має вигляд
 .
.
Використовуючи синдром, визначити помилку і декодувати прийняті комбінації 0110010, 1101001, 0111100, 0011110.
9 Твірна матриця лінійного блокового коду має вигляд
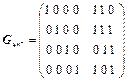 .
.
Визначити, які з комбінацій 1101001, 0110011, 0111100, 0011110 містять помилку, виправити їх і декодувати.
10 Розглянути лінійний блоковий (k, n)-код, кодове слово якого утворюється за правилом u= (x1, x2, x3, x4, x1+x3+x4, x1+x2+x4, x2+x3+x4). Визначити перевірну матрицю коду і параметри n, k. Чому дорівнює мінімальна кодова відстань отриманого коду?
11 Розглянути лінійний блоковий (k, n)-код, кодове слово якого утворюється за правилом u= (x1, x2, x3, x4, x1+x2, x3+x4, x1+x3, x2+x4, x1 + x2 + x3 + x4). Побудувати твірну матрицю коду.
12 Побудувати твірну матрицю лінійного блокового коду, здатного виправляти поодинокі помилки при передачі 16 повідомлень. Визначити синдром виправлення поодиноких помилок кодом. Навести приклад виявлення і виправлення помилки.
Розділ 11 КОД ХЕММІНГА
Найпоширенішими систематичними лінійними блоковими кодами є коди Хеммінга, до яких належать коди з мінімальною кодовою відстанню dmin =3, здатні виправляти поодинокі помилки.
При передачі кодового слова по каналу зв'язку можливе виникнення однократної помилки у будь-якому з його елементів. Кількість таких ситуацій дорівнює n. Отже, для того щоб визначити місце виникнення помилки, кількість різних комбінацій перевірних елементів  повинна перевищувати кількість можливих помилкових ситуацій в коді плюс ситуація, коли помилки немає, тобто повинна виконуватися нерівність
повинна перевищувати кількість можливих помилкових ситуацій в коді плюс ситуація, коли помилки немає, тобто повинна виконуватися нерівність
 . (3.9)
. (3.9)
З цієї нерівності випливає мінімальне співвідношення перевірних і інформаційних розрядів, необхідне для виправлення кодом поодиноких помилок
 . (3.10)
. (3.10)
Для розрахунку основних параметрів коду Хеммінга можна задатися кількістю перевірних елементів r, тоді довжина кодових слів 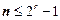 , а кількість інформаційних елементів k=n-r. Співвідношення між r, n і k зручно подати у вигляді такої таблиці (табл. 3.3).
, а кількість інформаційних елементів k=n-r. Співвідношення між r, n і k зручно подати у вигляді такої таблиці (табл. 3.3).
Таблиця 3.3
| k | |||||||||||||||
| r | |||||||||||||||
| n |
Характерною властивістю перевірної матриці лінійного блокового коду з dmin = 3 є те, що її стовпці являють собою різні ненульові комбінації завдовжки r.
Хеммінгомзапропоновано розміщувати стовпці перевірної матриці 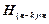 так, щоб i -й стовпець матриці, що відповідає номеру i помилкового розряду кодової комбінації,був двійковим поданням цього номера. Тоді синдромвиправлення однократних помилок кодом Хеммінга є двійковим поданням номера розряду, в якому виникла помилка. Для цього перевірні розряди, що відповідають стовпцям одиничної підматриці перевірної матриці коду, повинні знаходитися не в правій частині кодового слова, а у позиціях з номерами степеня двійки, тобто 20, 21, 22,…,
так, щоб i -й стовпець матриці, що відповідає номеру i помилкового розряду кодової комбінації,був двійковим поданням цього номера. Тоді синдромвиправлення однократних помилок кодом Хеммінга є двійковим поданням номера розряду, в якому виникла помилка. Для цього перевірні розряди, що відповідають стовпцям одиничної підматриці перевірної матриці коду, повинні знаходитися не в правій частині кодового слова, а у позиціях з номерами степеня двійки, тобто 20, 21, 22,…,  .
.
Наприклад, для r =3 перевірна матриця Хеммінга має вигляд
 .
.
Для даного лінійного блокового (4, 7)- коду перший, другий, четвертий розряди (u1, u2, u4) будуть перевірними, а третій, п'ятий, шостий і сьомий розряди (u3, u5, u6, u7) - символами інформаційного повідомлення у звичайному порядку, тобто (m1, m2m3, m4) відповідно.
Отже, для (k, n)- коду Хеммінга в кожному кодовому слові u =(u1, u2, u3, u4, …, u8, … un), r = n-k бітів з номерами степеня двійки є перевірними, а інші – бітами повідомлення, тобто кодування здійснюється так:
E (m1, m2, …, mk) =(u1, u2, …, un) =(r1, r2, m1, r3, m2, m3, m4, r4,
m5, m6, …, mk).
Перевірна матриця (k, n)- коду Хеммінга складається із r рядків і 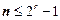 стовпців, що є двійковими комбінаціями числа i, де i - номер стовпця. Наприклад, для r = 2, 3, 4 перевірні матриці коду Хеммінга мають вигляд
стовпців, що є двійковими комбінаціями числа i, де i - номер стовпця. Наприклад, для r = 2, 3, 4 перевірні матриці коду Хеммінга мають вигляд
 ;
;  ;
;
 .
.
Синдром, що визначає систему перевірних рівнянь коду, знаходиться із рівняння
u ´  = 0.
= 0.
Наприклад, для r = 3 система перевірних рівнянь буде така:

Звідси визначають перевірні розряди (контрольні суми)

Щоб закодувати повідомлення m ® u, значеннями розрядів ui, де i не дорівнює степеню двійки, будуть відповідні біти повідомлення у тому самому порядку, а перевірні розряди з індексами степеня двійки знаходяться з системи перевірних рівнянь. У кожне рівняння системи входить тільки одна контрольна сума.
Приклад 1 Закодуємо повідомлення m= (0111) (4, 7)-кодом Хеммінга.
Кодовим словом для заданого повідомлення m буде послідовність u= (u 1 u 2 0 u 4 1 1 1), де u 1, u 2, u 4 - контрольні суми r1, r2, r3 відповідно.
Знаходимо контрольні суми з системи перевірних рівнянь:
r1 = u1 = u3 + u5 + u7 = m1 + m2 + m4 =0+1+1=0, r2 = u2 = u3 + u6 + u7 = m1 + m3 + m4 = 0+1+1=0, r3 = u4 = u5 + u6 + u7 = m2 + m3 + m4 = 1+1+1=1.
Отже, кодовим словом буде послідовність u= (0001111).
Декодування коду Хеммінга здійснюється у такий спосіб. Обчислюється синдром прийнятої послідовності y:
S = y ´  ,
,
де  - перевірна матриця коду. Якщо синдром нульовий вектор, то вважається, що слово передане без помилок, інакше значення синдрому відповідає двійковому поданню номера помилкового розряду. У цьому випадку потрібно змінити значення помилкового біту, нумеруючи біти зліва направо, починаючи з 1.
- перевірна матриця коду. Якщо синдром нульовий вектор, то вважається, що слово передане без помилок, інакше значення синдрому відповідає двійковому поданню номера помилкового розряду. У цьому випадку потрібно змінити значення помилкового біту, нумеруючи біти зліва направо, починаючи з 1.
Приклад 2 Повідомлення кодується (4, 7)- кодом Хеммінга. Декодуємо прийняту послідовність y= (0011111).
Обчислюємо синдром прийнятого вектора:
y ´  = (0011111)´
= (0011111)´ 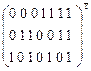 = (011)2 = 3 10 - помилка виникла у 3-му біті.
= (011)2 = 3 10 - помилка виникла у 3-му біті.
Виправляємо помилку, змінюючи значення у помилковому біті: (00 1 1111) ® (0001111).
Передане повідомлення декодується так:
D (u1, u2, u3, u4, u5, u6, u7)= D (0001111)=(0111).
Твірна матриця ( k, n )- коду Хеммінга - це матриця(k × n), в якій стовпці з номерами нестепеня 2 утворюють одиничну підматрицю, а решта стовпців визначається з перевірних рівнянь коду. Така матриця при кодуванні копіюватиме біти повідомлення у позиції з номерами нестепеня 2 і заповнюватиме інші позиції коду згідно з перевірним рівнянням знаходження відповідного контрольного розряду.
Приклад 3 Система перевірних рівнянь (4, 7)- коду Хеммінга має вигляд:
r1 = u1 = u3 + u5 + u7 = m1 + m2 + m4 ,
r2 = u2 = u3 + u6 + u7 = m1 + m3 + m4,
r3 = u4 = u5 + u6 + u7 = m2 + m3 + m4.
Відповідно твірна матриця даного коду така:
 .
.
Зразки розв'язування задач до розділу 11
Приклад 1 Закодувати повідомлення 11001010110 двійковим кодом Хеммінга. Побудувати твірну матрицю коду. Навести приклад виправлення помилки і декодування повідомлення. Визначити надлишковість коду.
Date: 2015-11-15; view: 1068; Нарушение авторских прав