Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Розв'язання
|
|
Синдром виправлення поодиноких помилок циклічним кодом визначається діленням многочлена вектора помилок на твірний поліном коду.
Припустимо, що кодується повідомлення m довжиною k символів – йому відповідає многочлен m (x) степеня k - 1.
Кодовим словом на виході кодера буде послідовність u довжиною n символів, якій відповідає многочлен u (x) степеня n-1.
Позначимо через e = (e0, e1, …, en-1 ) – вектор помилок в двійковому каналі зв'язку; s =(s0, s1, …, sn-k-1) – кодовий синдром, що визначається вектором помилок.
Вектор помилок подається многочленом вигляду e(x)=e0+e1x+…+en-1xn-1, а синдром – многочленом s(x)=s0+s1x+…+sn-k-1xn-k-1.
Знайдемо значення синдрому виправлення поодиноких помилок заданим циклічним (4, 7)- кодом:
1) е =(1000000) ® e (x)= 1,
1 x 3 + x + 1
s(x)= 1 ® (100);
2) е =(0100000) ® e (x)= x,
x x 3 + x + 1
s(x)= x ® (010);
3) е =(0010000) ® e (x)= x2,
x2 x 3 + x + 1
s(x)= x2 ® (001);
4) e =(0001000) ® e (x)= x3,
x3 x 3 + x + 1
+ x 3 + x + 1 1
x + 1
s(x)= 1+ x ® (110);
5) e =(0000100) ® e (x)= x4,
x4 x 3 + x + 1
+ x 4 + x2 + x x
x2 + x
s(x)= x + x2 ® (011);
6) e =(0000010) ® e (x)= x5,
x5 x 3 + x + 1
+ x 5 + x3 + x2 x2 +1
x3+ x2
+ x 3+ x + 1
x 2 + x + 1
s(x)= 1+x+x2 ® (111);
7) e =(0000001) ® e (x)= x6,
x6 x 3 + x + 1
+x 6 + x4 + x3 x3+ x + 1
x4 + x3
+ x 4 + x2 + x
x3 + x 2 + x
+x 3 + x + 1
x 2 + 1
s(x)= 1+x2 ® (101).
Знайдені комбінації синдрому є стовпцями перевірної матриці:
.
|
|
З перевірної матриці знаходимо твірну матрицю коду
.
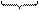
Кодове слово утворюється послідовністю u =(r0, r1, r2, m0, m1, m2, m3), де r0, r1, r2 – перевірочні символи.
Декодуємо задане повідомлення y= (1001110).
Даній послідовності відповідає поліном
y (x)= 1 × x 0 + 0 × x 1 + 0 × x 2 + 1 × x3 + 1 × x 4 + 1 × x 5+ 0 × x 6= 1 + x3 + x 4 + x 5.
Скористаємося алгоритмом декодування циклічних кодів:
1) 
Знайдемо остачу від ділення многочлена прийнятої комбінації на твірний поліном коду і тим самим перевіримо її на наявність помилки:
x 5+ x 4+ x 3 + 1 x 3 + x + 1
+ x5 + x3 + x2 x2 + x
x4+ x 2 + 1
+ x4 + x2 + x
x + 1
s(x)= 1+ x ® (110).
Ненульова остача s (x) свідчить про наявність помилки в прийнятій комбінації.
Вага остачі w (110)= 2 > l, де l = 1 – кратність помилок, що виправляються кодом, отже, необхідно виконати циклічний зсув кодованої послідовності на 1 розряд вправо:
(1001110) ® (0100111)® y (x)= 0 × x 0 + 1 × x 1 + 0 × x 2 + 0 × x3 +
+ 1 × x 4 + 1 × x 5+ 1 × x 6= x + x 4 + x 5 + x6.
2) Розділимо отриманий у результаті циклічного зсуву многочлен на твірний поліном коду:
x 6+ x 5+ x 4 + x x 3 + x + 1
+x6 + x4 + x3 x3 + x2
x5 + x 3 + x
+x5 + x3 + x2
x2 +x
s(x)= x + x2 ® (011).
Вага остачі w (011)= 2 > 1, отже, виконуємо циклічний зсув кодованої послідовності на 1 розряд вправо:
(0100111)® (1010011)® y (x)= 1 × x 0 + 0 × x 1 + 1 × x 2+ 0 × x3 + + 0 × x 4+ 1 × x 5+ 1 × x 6= 1+ x2 + x 5 + x6.
3) Розділимо отриманий у результаті циклічного зсуву многочлен на твірний поліном коду:
x 6+ x 5+ x 2 + 1 x 3 + x + 1
+x6 + x4 + x3 x3 + x2+x
x5+ x 4 + x3+ x2+ 1
+x5 + x3 + x2
x4+ 1
+x4+ x2+ x
x2+ x+ 1
s(x)= 1+ x + x2 ® (111).
Вага остачі w (111)= 3 > 1, знову виконуємо циклічний зсув кодованої послідовності й ділення її многочлена на твірний поліном коду: (1010011) ® (1101001) ®
® y (x)= 1 × x 0 + 1 × x 1 + 0 × x 2 + 1 × x3 + 0 × x 4 + 0 × x 5+ 1 × x 6= 1+ x + x 3 + x6.
4) Розділимо многочлен циклічно зсуненої послідовності на твірний поліном коду:
x 6 + x 3+ x + 1 x 3 + x + 1
+ x6+ x4 + x3 x3 + x
x 4 + x +1
+ x4 + x2 + x
x2+ 1
s(x)= 1+x2 ® (101).
Вага остачі w (101) = 2 > 1, виконуємо циклічний зсув й ділення на твірний поліном: (1101001) ® (1110100)® ® y (x)= 1 × x 0 + 1 × x 1 + 1 × x 2 + 0 × x3 + 1 × x 4 + 0 × x 5+ 0 × x 6= 1+ x + x 2 + x4.
5) Знову розділимо многочлен послідовності, отриманої у результаті останнього циклічного зсуву, на твірний поліном:
x 4+ x 2+ x + 1 x 3 + x + 1
+ x4 + x2 + x x
1
s(x)=1 ® (100).
Вага отриманої остачі w (100)= 1 £ 1, виконуємо дії з виправлення помилки.
Для цього додаємо до останнього циклічно зсунутого многочлена його остачу від ділення на твірний поліном:
x 4+ x 2+ x + 1+ 1 = x+ x 2+ x 4 ®(0110100).
Виконуємо циклічний зсув отриманої кодової комбінації у зворотному напрямку на 4 розряди вліво:
(0110100) ® (1000110).
Одержуємо виправлену кодову комбінацію u =(1000110).
Декодуємо передану послідовність, вилучивши перевірні елементи в лівій частині кодового слова: (1000110)®(0110).
Задачі до розділу 12
1 Поліноміальний код заданий твірним многочленом g(x)=1+x+x5+x 7. Закодувати повідомлення 0100, 10001101, 11110.
2 Поліноміальний (3, 6) - код заданий многочленом вигляду g(x)=1+x2+x 3. Побудувати твірну матрицю коду і таблицю декодування з виправленням помилки.
3 Закодувати циклічним кодом, здатним виправляти поодинокі помилки, комбінацію 011011. Навести приклад виправлення помилки в кодовій комбінації. Визначити надлишковість коду.
4 Циклічний (11, 15)- код заданий твірним поліномом вигляду g(x)=1+x 3 +x 4. Побудувати твірну матрицю коду. Навести приклад виправлення помилки даним кодом.
5 Побудувати перевірну матрицю циклічного (11, 15)- коду, заданого твірним поліномом g(x)=1+x+x 4. Виправити помилкову комбінацію 010111101011111 (біти пронумеровані зліва направо).
6 Побудувати перевірну матрицю циклічного (11, 15)- коду, заданого твірним поліномом вигляду g(x)=1+x+x 4. Закодувати послідовність 10010111011 (біти пронумеровані зліва направо). Скільки помилок у прийнятій комбінації може виявити і виправити код?
7 Циклічний (3, 7)- код заданий твірним поліномом вигляду g(x)=1+x+x2+x 4. Визначити мінімальну кодову відстань Хеммінга і здатність коду виявляти і виправляти помилки. Знайти ймовірність невиявлення помилки кодом, якщо ймовірність помилкової передачі біта повідомлення в каналі q=10-4.
8 Циклічний (4, 15)- код заданий твірним поліномом вигляду g(x)=1+x+x2+x3+x5+x7+x8+x 11. Закодувати комбінації 1100, 0011. Визначити мінімальну кодову відстань Хеммінга і здатність коду виявляти і виправляти помилки. Знайти ймовірність невиявлення помилки кодом, якщо ймовірність помилки в каналі q=10-2.
9 Циклічний код заданий твірним поліномом вигляду g(x)=1+x2+x3. Визначити і виправити помилкові комбінації 0111011, 1011010, 0010110 (біти пронумеровані зліва направо).
10 Циклічний код заданий твірним поліномом вигляду g(x)=1+x+x 3. Визначити і виправити помилкові комбінації коду: 0111011, 1011101, 0011010 (біти пронумеровані зліва направо).
11 Визначити синдром виправлення помилок циклічним (11, 15)- кодом, заданим твірним поліномом g(x)=1+x3+x 4. Побудувати перевірну і твірну матриці коду.
12 Декодувати повідомлення 1101011, 1110011, закодовані циклічним кодом, заданим твірним поліномом g(x)=1+x2+x3+x4, виправивши помилку, якщо вона є (біти пронумеровані зліва направо).
13 Закодувати циклічним кодом, заданим твірним поліномом вигляду g(x)=1+x+x3+x4, комбінацію m (x)= 1 + x4 + x7. Навести приклад виправлення помилки даним кодом. Визначити його надлишковість.
14 Закодувати циклічним кодом, здатним виправляти поодинокі помилки, комбінацію 0111. Навести приклад виправлення помилки в кодовій комбінації. Визначити надлишковість коду.
15 Циклічний (4, 7)- код заданий твірним поліномом вигляду g(x)=1+x+x3. Знайти перевірний поліном коду, за його допомогою закодувати комбінації 011, 110, 101. Навести приклад виправлення помилки отриманим циклічним кодом.
Контрольні запитання до розділів 9-12
1 Які коди належать до завадостійких? Якими загальними властивостями вони характеризуються?
2 Для чого в завадостійкі коди вводиться надлишковість?
3 Які існують класи завадостійких кодів?
4 Які коди належать до блокових завадостійких кодів? В яких випадках їх доцільно використовувати?
5 У чому полягає відмінність блокових і згорткових кодів?
6 Як визначаються операції додавання та множення за модулем 2 у полі двійкових символів GF(2)?
7 Які коди належать до лінійних блокових кодів? Які коди мають властивість систематичності?
8 У чому полягає принцип кодування з перевіркою на парність? Яка надлишковість коду? У чому переваги та недоліки кодування?
9 Який канал передачі інформації описується моделлю двійкового симетричного каналу?
10 У чому полягає принцип виявлення і виправлення помилок ітеративним кодом? Які переваги та недоліки такого кодування?
11 Які існують способи задання лінійних блокових кодів? Які основні частини мають кодові слова лінійного блокового коду?
12 Що таке система перевірних рівнянь лінійного блокового коду?
13 Що таке твірна матриця лінійного блокового коду? Які її властивості? Яка структура твірної матриці?
14 Як, скориставшись твірною матрицею, побудувати систему перевірних рівнянь лінійного блокового коду?
15 Що таке перевірна матриця лінійного блокового коду? Які її властивості? Яка структура перевірної матриці?
16 Як, скориставшись перевірною матрицею, побудувати систему перевірних рівнянь лінійного блокового коду?
17 Як визначається вектор помилок у двійковому каналі зв'язку? У чому полягає задача декодування переданого кодового слова?
18 Що таке кодовий синдром лінійного коду? Як він визначається?
19 Яку властивість має кодовий синдром прийнятої кодованої послідовності? У яких випадках синдром не дозволяє знайти помилки у переданій послідовності?
20 Яким чином за допомогою кодового синдрому виявляються та виправляються помилки лінійним блоковим кодом?
21 Як визначаються вага і відстань Хеммінга для двійкових послідовностей?
22 Що таке мінімальна кодова відстань Хеммінга лінійного блокового коду? Як вона визначається?
23 Як записуються необхідна і достатня умови виявлення лінійним блоковим кодом помилок заданої кратності?
24 Як записуються необхідна і достатня умови виправлення лінійним блоковим кодом помилок заданої кратності?
25 Які необхідна і достатня умови існування завадостійкого коду?
26 Як визначається мінімальна кількість перевірних символів для лінійного блокового коду із заданими характеристиками?
27 Як побудувати твірну матрицю лінійного блокового коду із заданими характеристиками?
28 Які лінійні блокові коди називаються кодом Хеммінга?
29 Як знаходиться кількість інформаційних і перевірних символів для коду Хеммінга?
30 Як утворюються кодові слова коду Хеммінга?
31 Як складається перевірна матриця коду Хеммінга?
32 Як виконується декодування коду Хеммінга?
33 Як складається твірна матриця коду Хеммінга?
34 У чому полягає принцип поліноміального кодування?
35 Як визначаються основні арифметичні операції над поліномами в полі двійкових символів GF(2)?
36 Які коди називаються поліноміальними?
37 Що таке твірний поліном коду? Які властивості він має?
38 Яким чином виявляються помилки поліноміальним кодом? В яких випадках помилки залишаються не знайденими?
39 Як побудувати твірну матрицю поліноміального коду?
40 Які поліноміальні коди називаються циклічними? Які їх властивості?
41 У чому полягає алгоритм кодування циклічним кодом?
42 Що таке перевірний поліном циклічного коду? Які його властивості?
43 Як визначається поліном синдрому для циклічних кодів?
44 Як зв'язаний поліном синдрому з поліномом помилок у каналі?
45 Як побудувати твірну та перевірну матриці циклічного коду?
46 Як виявляються і виправляються помилки циклічним кодом?
47 У чому полягає алгоритм декодування циклічного коду на основі прийняття або відхилення гіпотез?
48 У чому полягає алгоритм декодування циклічних кодів, що використовує послідовний циклічний зсув елементів кодованої послідовності?
Відповіді до задач
Date: 2015-11-15; view: 583; Нарушение авторских прав