
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розв'язання. а)Розпакуємо код повідомлення, стиснутого за алгоритмом LZ78 (табл
|
|
а)Розпакуємо код повідомлення, стиснутого за алгоритмом LZ78 (табл. 1):
Таблиця 1
| Вхідний код | Вихідна фраза (словник) | Позиція словника |
| “” | ||
| <0, ‘ A ’> | “A” | |
| <0, ‘ F ’> | “F” | |
| <0, ‘ X ’> | “X” | |
| <1, ‘ F ’> | “AF” | |
| <2, ‘ X ’> | “FX” | |
| <5, ‘ A ’> | “FXA” | |
| <3, ‘ A ’> | “XA” | |
| <2, ‘ F ’> | “FF” | |
| <0, ‘ A ’> | “A” |
Отже, розкодовано повідомлення AFXAFFXFXAXAFFA.
Довжина стиснутого повідомлення 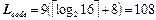 (бітів).
(бітів).
Довжина нестиснутого повідомлення LASCII+ =15×8=120 (бітів).
б) Розпакуємо повідомлення за алгоритмом LZW (табл.2):
Таблиця 2
| Вхідний код | Вихідна фраза | Словник | Позиція словника |
| ASCII+ | 0 – 255 | ||
| 0‘ A ’ | “A” | “AF” | |
| 0‘ F ’ | “F” | “FX” | |
| 0‘ X ’ | “X” | “XA” | |
| <256> | “AF” | “AFF” | |
| <257> | “FX” | “FXF” | |
| <257> | “FX” | “FXA” | |
| 0‘ A ’ | “A” | “AX” | |
| <258> | “XA” | “XAF” | |
| 0‘ F ’ | “F” | “FF” | |
| 0‘ F ’ | “F” | “FA” | |
| 0‘ A ’ | “A” |
Отже, закодовано повідомлення AFXAFFXFXAXAFFA.
Довжина стиснутого повідомлення Lcode =11*9=99 (бітів).
Задачі до розділу 7
1 Закодувати повідомлення AABCDAACCCCDBB, використовуючи словникові алгоритми стиснення LZ77 і LZSS (словник - 12 байтів, буфер – 4 байти). Обчислити довжину у бітах отриманих кодів.
2 Закодувати повідомлення КИБЕРНЕТИКИ, використовуючи словникові алгоритми стиснення LZ77 і LZSS (словник - 12 байтів, буфер – 4 байти). Обчислити довжину у бітах отриманих кодів.
3 Закодувати повідомлення СТРАННЫЙ СТРАННИК, використовуючи словникові алгоритми стиснення LZ77 і LZSS (словник - 12 байтів, буфер – 4 байти). Обчислити довжину у бітах отриманих кодів.
4 Закодувати повідомлення BDCBDDCDCBCBDDBDBDBC, використовуючи словникові алгоритми стиснення LZ77 і LZSS (словник - 12 байтів, буфер – 4 байти). Обчислити довжину у бітах отриманих кодів.
5 Розпакувати повідомлення і обчислити довжину їх кодів:
а) повідомлення стиснуте за алгоритмом LZ77 (словник – 12 байтів, буфер – 4 байти), код повідомлення такий: á0, 0, ‘ A ’ñ á11, 1, ‘ B ’ñ á0, 0, ‘ C ’ñ á0, 0, ‘ D ’ñ á7, 2,‘ C ’ñ á11,1,‘ C ’ñ á5, 2, ‘ B ’ñ á0, 0, ‘ B ’ñ;
б) повідомлення стиснуте за алгоритмом LZSS (словник – 12 байтів, буфер – 4 байти), код повідомлення такий: 0‘ A ’ 1á11, 1ñ 0‘ B ’ 0‘ C ’ 0‘ D ’ 1á7, 2ñ 1á8, 1ñ 1á11, 1ñ 1á10, 2ñ 1á5, 1ñ 1á2, 1ñ 1á11, 1ñ.
6 Розпакувати повідомлення і обчислити довжину їх кодів:
а) повідомлення стиснуте за алгоритмом LZ77 (словник – 12 байтів, буфер – 4 байти), код повідомлення: á0,0,‘ / ’ñ á0,0,‘ W ’ñ á0,0,‘ E ’ñ á0,0,‘ D ’ñ á8,3,‘ / ’ñ á5,4,‘ W ’ñ á8,1,‘ B ’ñ á8,3,‘ E ’ñ á4,4,‘ / ’ñ á4,4,‘ E ’ñ;
б) повідомлення стиснуте за алгоритмом LZSS (словник – 12 байтів, буфер – 4 байти), код повідомлення такий: 0‘ / ’ 0‘ W ’ 0‘ E ’ 0‘ D ’ 1á8,3ñ 1á5,4ñ 1á8,3ñ 0‘ B ’ 1á8,3ñ 1á0,4ñ 1á4,4ñ 1á4,2ñ 1á10,1ñ.
7 Розпакувати повідомлення і обчислити довжину їх кодів:
а) Повідомлення стиснуте за алгоритмом LZ77 (словник – 12 байтів, буфер – 4 байти), код повідомлення á0,0,‘ В ’ñ á0,0,‘ О ’ñ á0,0,‘’ñ á0,0,‘ Д ’ñ á8,2,‘ Р ’ñ á0,0,‘ Е ’ñ á6,1,‘ Т ’ñ á8,1,‘ А ’ñ á4,1,‘ А ’ñ á6,1,‘ Н ’ñ á9,2,‘ Т ’ñ á3,3,‘ Е ’ñ á6,1,‘ Д ’ñ á6,1,‘ О ’ñ á6,1,‘ А ’ñ;
б) Повідомлення стиснуте за алгоритмом LZSS (словник – 12 байтів, буфер – 4 байти), код повідомлення 0‘ В ’ 0‘ О ’ 0‘’ 0‘ Д ’ 1<8,2>0‘ Р ’ 0‘ Е ’1<6,1>0‘ Т ’ 1<8,1>0‘ А ’1<4,1>1<10,1>1<6,1>0‘ Н ’ 1<9,2> 1<3,4> 0‘ Е ’ 1<6,1> 0‘ Д ’ 1<6,1> 0‘ О ’ 1<6,1> 1<4,1>.
8 Закодувати повідомлення AABCDAACCCCDBB, використовуючи словникові алгоритми стиснення LZ78 (словник - 16 фраз) і LZW (словник – ASCII+ і 16 фраз). Обчислити довжину отриманих кодів.
9 Закодувати повідомлення КИБЕРНЕТИКИ, використовуючи словникові алгоритми стиснення LZ78 (словник - 16 фраз) і LZW (словник – ASCII+ і 16 фраз). Обчислити довжину отриманих кодів.
10 Закодувати повідомлення СТРАННЫЙ СТРАННИК, використовуючи словникові алгоритми LZ78 (словник - 16 фраз) і LZW (словник – ASCII+ і 16 фраз). Обчислити довжину у бітах отриманих кодів.
11 Закодувати повідомлення BDCBDDCDCBCBDDBDBDBC, використовуючи словникові алгоритми LZ78 (словник - 16 фраз) і LZW (словник – ASCII + і 16 фраз). Обчислити довжини у бітах отриманих кодів.
12 Розпакувати повідомлення і обчислити довжину їх кодів:
а) повідомлення стиснуте за алгоритмом LZ78 (словник – 16 фраз). Код повідомлення такий: á0,‘ A ’ñ á1,‘ B ’ñ á0,‘ C ’ñ á0,‘ D ’ñ á1,‘ А ’ñ á3,‘ C ’ñ á6,‘ D ’ñ á0,‘ B ’ñ á0,‘ B ’ñ;
б) повідомлення стиснуте за алгоритмом LZW (словник ASCII+ і 16 фраз). Код повідомлення такий: 0‘ A ’ 0‘ A ’ 0‘ B ’ 0‘ C ’ 0‘ D ’ á256ñ 0‘ C ’ á262ñ á259ñ 0‘ B ’ 0‘ B ’.
13 Розпакувати повідомлення і обчислити довжину їх кодів:
а) повідомлення стиснуте за алгоритмом LZ78 (словник – 16 фраз). Код стиснутого повідомлення: á0,‘ / ’ñ á0,‘ W ’ñ á0,‘ E ’ñ á0,‘ D ’ñ á1,‘ W ’ñ á3,‘ / ’ñ á2,‘ E ’ñ á4,‘ / ’ñ á7,‘ B ’ñ á5,‘ E ’ñ á6,‘ W ’ñ á3,‘ B ’ñ á10,‘ E ’ñ á1,‘ E ’ñ;
б) повідомлення стиснуте за алгоритмом LZW (словник ASCII+ і 16 фраз). Код стиснутого повідомлення такий: 0‘ / ’ 0‘ W ’ 0‘ E ’ 0‘ D ’ á256ñ 0‘ E ’ á260ñ á259ñ á257ñ 0‘ B ’ á260ñ á261ñ á264ñ á266ñ 0‘ / ’ 0‘ E ’.
14 Розпакувати повідомлення і обчислити довжину їх кодів:
а) повідомлення стиснуте за алгоритмом LZ78 (словник – 32 фрази). Код стиснутого повідомлення такий: á0,‘ В ’ñ á0,‘ О ’ñ á0,‘ ’ñ á0,‘ Д ’ñ á1,‘ О ’ñ á0,‘ Р ’ñ á0,‘ E ’ñ á3,‘ Т ’ñ á6,‘ А ’ñ á1,‘ А ’ñ á3,‘ Н ’ñ á0,‘ А ’ñ á8,‘ Р ’ñ á12,‘ В ’ñ á7,‘’ñ á4,‘ Р ’ñ á2,‘ В ’ñ á0,‘ А ’ñ;
б) повідомлення стиснуте за алгоритмом LZW (словник ASCII+ і 32 фрази).Код стиснутого повідомлення такий: 0‘ В ’ 0‘ О ’0‘’0‘ Д ’á256ñ 0‘ Р ’ 0‘ Е ’ 0‘’ 0‘ Т ’ 0‘ Р ’ 0‘ А ’ 0‘ В ’ 0‘ А ’ 0‘’ 0‘ Н ’ á268ñ á264ñ á266ñ á262ñ 0‘ Д ’ 0‘ Р ’ 0‘ О ’ á267ñ.
Розділ 8 СИСТЕМИ СТИСНЕННЯ ІНФОРМАЦІЇ
8.1 Огляд типів систем стиснення інформації
Передача і зберігання інформації потребує достатньо значних витрат. Велика частина даних, що потрібно передавати по каналах зв'язку або зберігати, має не найкомпактніше подання. Звичайно, дані зберігаються у формі, що забезпечує їх найпростіше використовування, наприклад: звичайні книжкові тексти, ASCII -коди текстових редакторів, двійкові коди даних ЕОМ, відліки сигналів в інформаційно-вимірювальних системах і т. ін. Проте таке подання даних вимагає удвічі-втричі, а іноді і у сотні разів більше місця для збереження і ширшу смугу частот для передачі, ніж це насправді потрібно. Тому стиснення даних є одним із найактуальніших напрямів розвитку цифрових систем передачі та збереження інформації. На сьогодні більшість з цих систем просто не змогли б успішно функціонувати без економного кодування. Не було б цифрового сотового зв'язку стандартів GSM та CDMA, цифрового супутникового телебачення, дуже неефективною була б робота в Internet, не говорячи вже про необхідність стиснення зображень, музики, відео і т. ін.
Узагальнену схему системи стиснення інформації можна подати у такому вигляді (рис.2.11).

Рисунок 2. 11
Кодер джерела перетворює дані до стисненого вигляду, а декодер їх відновлює. Відновлені дані можуть або точно збігатися з початковими, або трохи від них відрізнятися.
З огляду на розмаїтість наявних типів систем і методів стиснення інформації розглянемо лише деякі з них.
Системи стиснення інформації поділяються за їхнім функціональним призначенням, степенем і швидкістю перетворення даних, степенем їхнього відновлення.
За функціональним призначенням вирізняють системи стиснення для передачі даних і для їхньої архівації. Різниця полягає у тому, що перші діють з незначними за обсягами даними (до декількох десятків і сотень байтів), а інші - із набагато більшим обсягом інформації (мегабайти).
За характером стиснення даних вирізняють лінійні, матричні, комбіновані і каскадні способи стиснення.
До лінійних належать такі способи стиснення, за якими кодування виконується в одному напрямі (горизонтальному або вертикальному).
До матричних належать способи стиснення, за якими використовується матричний принцип заміни повторюваних елементів інформаційного масиву.
До комбінованих належать системи стиснення, в яких використовуються два або більше лінійних або матричних способів стиснення.
До каскадних належать системи послідовного стиснення інформації різними способами.
За степенем стиснення вирізняють низькоефективні (з коефіцієнтом стиснення r < 1,5), середньоефективні (r=1, 5...3) і високоефективні (r > 3) системи. Так само за швидкістю перетворення інформації системи стиснення поділяють на низько -, середньо - і високошвидкісні, для яких швидкість R змінюється відповідно від кількох кілобайтів до мегабайтів за секунду.
При використовуванні двійкового кодування інформації коефіцієнт стиснення визначається відношенням розміру початкових даних до розміру стиснених даних у бітах:
 , (2.15)
, (2.15)
де через dim (X) позначено об'єм алфавіту джерела X; n - довжина початкового повідомлення (у символах); k - довжина стисненого повідомлення у бітах.
Відповідно швидкість стиснення визначають так:
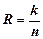 (2.16)
(2.16)
і вимірюють як кількість бітів коду, що припадає на одне елементарне повідомлення джерела, тобто є середньою довжиною коду повідомлення завдовжки n.
Системи, що мають більший коефіцієнт стиснення, забезпечує меншу його швидкість.
За степенем відновлення інформації вирізняютьсистеми стиснення без втрат інформації (неруйнуюче стиснення) тасистеми стиснення із втратами (руйнуюче стиснення).
Стисло розглянемо ці типи систем стиснення інформації.
8.2 Стиснення без втрат інформації
У системах стиснення без втратдекодер відновлює дані джерела абсолютно точно. Узагальнена схема системи стиснення без втрат інформації має такий вигляд (рис. 2.12):

Рисунок 2. 12
Вектор даних, що підлягає стисненню, є послідовністю  скінченної довжини. Елементарні повідомлення, що утворюють вектор
скінченної довжини. Елементарні повідомлення, що утворюють вектор  , обираються із скінченного алфавіту джерела X.
, обираються із скінченного алфавіту джерела X.
Виходом кодера є стиснені дані у вигляді двійкової послідовності 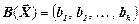 , довжина якої k залежить від
, довжина якої k залежить від  . Оскільки система стиснення неруйнуюча, то однаковим векторам
. Оскільки система стиснення неруйнуюча, то однаковим векторам  відповідають однакові кодові слова на виході кодера
відповідають однакові кодові слова на виході кодера  .
.
8.3 Стиснення із втратами інформації
У системах стиснення із втратамиінформації кодування здійснюється так, що декодер не в змозі відновити дані джерела в первинному вигляді. Узагальнена схема системи стиснення із втратами інформації зображена на рис. 2.13

На відміну від попередньої схеми (рис. 2.12) у цій схемі наявний квантователь, що перетворює вектори вхідних даних  на вектор
на вектор  достатньо близький до
достатньо близький до  за значенням середньоквадратичної помилки. Задача квантователя полягає у зменшенні розміру алфавіту джерела. Звичайно, на цьому етапі дані приводять до вигляду, в якому вони можуть бути ефективно стиснуті без втрат.
за значенням середньоквадратичної помилки. Задача квантователя полягає у зменшенні розміру алфавіту джерела. Звичайно, на цьому етапі дані приводять до вигляду, в якому вони можуть бути ефективно стиснуті без втрат.
Далі кодер піддає неруйнуючому стисненню вектор квантованих даних  так, щоб забезпечувалася однозначна відповідність між
так, щоб забезпечувалася однозначна відповідність між  і
і 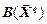 , тобто для будь-яких
, тобто для будь-яких  виконується умова
виконується умова  . Проте система в цілому залишається руйнуючою, оскільки двом різним векторам на вході може відповідати той самий відновлений вектор.
. Проте система в цілому залишається руйнуючою, оскільки двом різним векторам на вході може відповідати той самий відновлений вектор.
Руйнуючий кодер характеризується швидкістю стисненняR і величиною спотвореньD, що знаходяться за формулами:
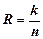 ,
,  . (2.17)
. (2.17)
Параметр R характеризує швидкість стиснення у бітах на одне елементарне повідомлення, а параметр D є мірою середньоквадратичної різниці  та
та 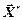 . Ці два параметри пов'язані зворотною залежністю.
. Ці два параметри пов'язані зворотною залежністю.
Вибір системи стиснення із втратами або без втрат залежить від типу даних, що стискаються. При стисненні текстів, документів, комп'ютерних програм, банківської інформації і т. ін. очевидно, що необхідно використовувати неруйнуюче стиснення, оскільки в цих випадках необхідне точне відновлення початкової інформації. А у тих випадках, коли інформація, що стискається, використовується лише для якісної її оцінки - це, як правило, аналогові дані, використовується стиснення із втратами, щовиявляється дуже доцільним, оскількипри практично непомітних спотвореннях стиснення із втратами забезпечує на порядок, а іноді і на два більшуйого швидкість. Зрозуміло, що стиснення із втратами забезпечує і істотно більший коефіцієнт стиснення порівняно із системами неруйнуючого кодування.
Контрольні запитання до розділів 3-8
1 Що таке економне кодування інформації? З якою метою воно здійснюється?
2 Які існують способи задання кодів?
3 Що таке рівномірні й нерівномірні коди?
4 З якою метою використовуються оптимальні нерівномірні коди?
5 Що таке надлишковість коду? Як вона визначається?
6 Яке кодування інформації називається статистичним? Які алгоритми стиснення даних відносять до статистичних?
7 Що таке оптимальне кодування інформації? Який критерій оптимальності статистичних кодів?
8 Які коди називаються префіксними? Що таке вектор Крафта? Як записується нерівність Крафта? У чому полягає умова оптимальності префіксних кодів?
9 У чому полягає алгоритм побудови птимального коду Шеннона-Фано?
10 У чому полягає алгоритм побудови оптимального коду Хаффмена?
11 Які переваги та недоліки використання оптимального кодування Шеннона-Фано і Хаффмена?
12 Чим визначається верхня границя стиснення інформації? Які існують границі стиснення при використанні оптимального кодування Шеннона-Фано і Хаффмена?
13 Які коди характеризуються «наявністю пам'яті»?
14 Які коди називаються блоковими? Що таке порядок блокового коду?
15 У чому полягає метод блокування повідомлень? Як будується блоковий код Хаффмена?
16 У чому полягає арифметичний алгоритм кодування інформації? Які його переваги в порівнянні з іншими статистичними методами стиснення інформації?
17 Як здійснюється декодування даних за арифметичним алгоритмом?
18 У чому полягає адаптивний алгоритм Хаффмена? Що таке упорядковане дерево Хаффмена?
19 Як здійснюється кодування/декодування вхідних даних за адаптивним алгоритмом Хаффмена?
20 Які переваги і недоліки адаптивного алгоритму Хаффмена?
21 У чому полягає основна ідея словникових методів стиснення інформації? У чому переваги використання словникових методів у порівнянні із статистичними?
22 На які основні групи поділяються словникові алгоритми стиснення? Які їх відмітні риси?
23 У чому полягають словникові методи стиснення з використанням «ковзного» вікна LZ77, LZSS? Чим визначається довжина кодів цих алгоритмів?
24 Які переваги модифікованого алгоритму LZSS у порівнянні з LZ77?
25 Які недоліки словникових алгоритмів LZ77, LZSS?
26 У чому полягають словникові методи стиснення LZ78, LZW? Чим визначається довжина кодів для цих алгоритмів? Які переваги модифікації LZW?
27 Які переваги алгоритмів LZ78, LZW у порівнянні з LZ77, LZSS?
28 Які основні елементи включає система стиснення інформації? Які функції вони виконують?
29 За якими ознаками класифікують системи й методи стиснення даних?
30 Чим відрізняються системи стиснення інформації, призначені для передачі й для архівації даних?
31 Які способи стиснення належать до лінійних, матричних, каскадних?
32 Як характеризуються системи стиснення інформації за ступенем і швидкістю стиснення?
33 Як знаходяться коефіцієнт та швидкість стиснення двійкових даних?
34 Які системи характеризуються стисненням без втрат інформації? Які основні елементи вони включають?
35 Які системи характеризуються стисненням із втратами інформації? У чому різниця систем із втратами й без втрат інформації?
36 Чим визначаються швидкість стиснення й величина спотворень у системах стиснення із втратами інформації?
| Частина III Завадостійке кодування інформації |
Розділ 9 ОСНОВНІ ПРИНЦИПИ ЗАВАДОСТІЙКОГО КОДУВАННЯ.
ЛІНІЙНІ БЛОКОВІ КОДИ
9.1 Основні принципи
Завадостійке кодування інформації використовується для підвищення надійності передачі по цифрових каналах.
Наведемо властивості завадостійких (коригувальних) кодів:
1) використання надлишковості - закодовані послідовності завжди містять додаткові надлишковісимволи;
2) усереднювання - надлишкові символи залежать від декількох інформаційних, тобто інформація, що міститься у кодовій послідовності, перерозподіляється й на надлишкові символи.
Завадостійкі коди поділяються на два великі класи: блокові і згорткові коди. Визначальна різниця між цими кодами – у відсутності або наявності пам'яті кодера.
Кодер для блокових кодів поділяє неперервну інформаційну послідовність на блоки завдовжки k символів. Кодер каналу перетворює блоки повідомлення X у більш довгі послідовності Y, що складаються з n символів й називаються кодовими словами. r=n-k символів, що додаються кодером до кожного блоку повідомлення, називають надлишковими, або перевірними, або контрольними. Вони не несуть додаткової інформації, їх функції полягають у забезпеченні можливостей виявлення й виправлення помилок, спричинених наявністю завад у каналі зв'язку.
k -розрядним двійковим словам можна поставити у відповідність 2k різних значень з алфавіту джерела, яким відповідатиме 2k кодових слів на виході кодера. Така множина 2k кодових слів називається блоковим кодом. Термін «без пам'яті» означає, що кожний блок з n символів залежить лише від відповідного k -символьного інформаційного блоку і не залежить від інших блоків повідомлення.
Кодердля згорткових кодів опрацьовує інформаційні послідовності без розбиття їх на незалежні блоки. У кожний момент часу кодер перетворює невелику послідовність з k інформаційних символів у блок з n кодових символів, де n>k. При цьому кодовий n -символьний блок залежить не тільки від k -символьного інформаційного блоку, наявного на вході у поточний момент часу, але і від попередніх m блоків повідомлення. У цьому і полягає наявність пам'яті кодера.
Блокові коди доцільно використовувати у тих випадках, якщо первинні дані згруповані у блоки або масиви.
Згорткові коди найчастіше використовуються для передачі по радіоканалах і краще підходять для побітової передачі даних. Крім того, при однаковій надмірності згорткові коди, як правило, мають кращу виправну здатність.
Однією з умов практичної реалізації блокового завадостійкого коду є умова його лінійності.
Визначення. Блоковий код завдовжки n символів, що складається з 2k кодових слів, називається лінійним(k, n) - кодом за умови, що усі його 2k кодових слів утворюють k -вимірний підпростір векторного простору n -послідовностей двійкового поля GF(2). Іншими словами, двійковий код є лінійним, якщо порозрядна сума за модулем 2 (mod 2) двох кодових слів також є кодовим словом даного коду.
Бажаною якістю лінійних блокових кодів є систематичність. Систематичний код має інформаційну частину з k символів і надмірну (перевірну) частину з n-k символів постійної довжини.
9.2 Елементи двійкової арифметики
Полем називається множина математичних об'єктів, для яких визначені операції додавання, віднімання, множення й ділення.
Розглянемо найпростіше поле з двох елементів 0 і 1. Визначимо для нього операції додавання і множення так:
| 0+0=0, 0+1=1, 1+0=1, 1+1=0; | 0*0=0, 0*1=0, 1*0=0, 1*1=1. |
Визначені таким чином операції додавання та множення називають додаванням та множенням за модулем 2 (mod 2).
З рівності 1+1=0 випливає, що -1=1 та 1+1=1-1, а з рівності 1*1=1, що 1:1=1.
Алфавіт з двох символів 0 і 1 з означеними для них операціями додавання й множення за mod 2 називається двійковим полем GF(2). Для поля GF(2) застосовні усі методи лінійної алгебри, у тому числі матричні операції.
Операція додавання за mod 2, як правило, позначається символом Å, проте у подальшому у даному курсі розглядається тільки додавання за mod 2, тому використовується звичайний знак +.
9.3 Код з перевіркою на парність
Найпростіший лінійний блоковий код - це (n-1, n) - код з контролем парності. Цей код, зокрема, широко використовується у модемах.
Кодування полягає у додаванні до кожного байта 9-го контрольного біта так, щоб доповнити кількість одиниць у байті до наперед вибраного для коду парного (even) або непарного (odd) значення.
Наприклад, задана інформаційна послідовність (101), тоді кодовим словом буде (1010), де перевірний символ знаходиться додаванням за mod 2 символів інформаційної послідовності. Якщо число одиниць в інформаційній послідовності парне, то значенням суми за mod 2 буде 0, якщо непарне - то 1, отже, перевірний символ доповнює кодову послідовність так, щоб кількість одиниць в ній була парною.
Математично схему кодування з перевіркою на парність можна записати так:
Е (m1,..., mk)=(m1,..., mk, mk+1),
де перевірний символ

Отже, кількість одиниць в прийнятій послідовності повинна бути парною, тобто  .
.
Схему декодування можна записати так:

Уведемо поняття двійкового симетричного каналу, для якого помилки у бітах рівноймовірні й незалежні. Схематично двійковий симетричний канал зображений на рис. 3.1, де р - ймовірність безпомилкової передачі біта повідомлення; q = 1-p - ймовірність помилкової передачі.
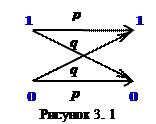 |
Для такої схеми передачі даних ймовірність того, що у n -позиційному коді виникне тільки одна помилка, становить  .
.
У загальному випадку ймовірність передачі n бітів з k помилками визначається за формулою Бернуллі
 (3.1)
(3.1)
де  - кількість сполук з n елементів по k.
- кількість сполук з n елементів по k.
Додамо, що код з перевіркою парності не виявляє помилки кратності 2, оскільки, якщо у переданій послідовності виникло 2, 4 і т. д. помилки, незалежно, в якій позиції, то загальне число одиниць в прийнятій послідовності стане парним, і помилки виявлені не будуть. Проте ймовірність двократної помилки значно менша, ніж поодинокої. Покажемо це на прикладі.
Приклад Перевірка парності при k =2 реалізується таким кодом: 00 → 000, 01 → 011, 10 → 101, 11 → 110.
Позначимо через р ймовірність правильної передачі, q – ймовірність помилки у біті повідомлення.
Тоді ймовірність виникнення хоча б однієї помилки у кодовій послідовності завдовжки 3 біти P=q3+3pq2+3p2q. З них не будуть виявлені помилки у двох бітах, що не змінюють парності, ймовірність яких Pпом=3pq2.
Ймовірність помилкової передачі повідомлення з двох бітів без використання контролю парності Pпом=q2+2pq.
Для достатньо надійного каналу передачі, тобто при q << 1, 3pq2 << q2+2pq, що свідчить про доцільність використання завадостійкого кодування з виявленням поодиноких помилок.
Не зважаючи на простоту і не дуже високу ефективність, коди з перевіркою на парність широко використовуються у системах передачі і зберігання інформації. Їх цінують за невисоку надлишковість: достатньо додати до інформаційної послідовності один перевірний символ - і можна визначити, чи є у прийнятій послідовності помилка. Проте локалізувати місце виникнення помилки, й відтак її виправити неможливо. Можна лише повторити передачу помилкової комбінації.
9.4 Ітеративний код
Припустимо, потрібно передати повідомлення m завдовжки 9 символів. Розмістимо символи повідомлення у вигляді матриці, додавши до кожного рядка і стовпця контрольні символи перевірки на парність (табл. 3.1).
Таблиця 3.1
| m 1 | m 2 | m 3 | m 1+ m 2+ m 3 |
| m 4 | m 5 | m 6 | m 4+ m 5+ m 6 |
| m 7 | m 8 | m 9 | m 7+ m 8+ m 9 |
| m 1+ m 4+ m 7 | m 2+ m 5+ m 8 | m 3+ m 6+ m 9 | m 1+ m 2+...+ m 9 |
Якщо у процесі передачі в цій таблиці виникне одна помилка, то перевірка на парність у відповідному рядку і стовпці не виконуватиметься. Координати помилки однозначно визначаються номерами стовпця і рядка, в яких не виконується перевірка на парність. Відтак, такий код може не тільки виявляти, але й виправляти помилки.
Описаний метод кодування називається ітеративним. Його застосування доцільне, якщо дані формуються у вигляді масивів, наприклад, в шинах ЕОМ, в пам'яті, що має табличну структуру.
Недоліком такого кодування є значна надлишковість при порівняно низькій виправній здатності.
Зразки розв'язування задач до розділу 9
Приклад 1 Завадостійкий код заданий твірною матрицею вигляду
 .
.
1) Побудувати таблицю кодів;
2) Описати основні характеристики коду: мінімальну відстань між словами, ймовірність невиявлення помилки, максимальну кратність помилок, які можуть бути виявлені й виправлені кодом;
3) Побудувати таблицю декодування;
4) Уточнити можливості коду з виявлення і виправлення помилок: знайти ймовірність правильної передачі закодованого повідомлення і описати помилки, що виправляються кодом;
5) Як будуть декодовані слова: 10001, 01110, 10111?
Date: 2015-11-15; view: 787; Нарушение авторских прав