Розв'язання. Інформаційну послідовність розмістимо у вигляді матриці розмірністю 3´4

Інформаційну послідовність розмістимо у вигляді матриці розмірністю 3´4. Дописуємо до кожного рядка і стовпця матриці перевірний елемент контролю на парність.

У загальному вигляді такий спосіб кодування інформаційної послідовності (m ₁, m ₂, …, m ₁₂) подамо так:

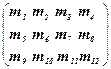Þ , (*)

де r ₁, r ₂, …, r ₈ – перевірні елементи.

Записавши матрицю (*) по рядках, отримуємо послідовність, що зберігається або передається по каналу зв’язку, u= (m ₁, m ₂, m ₃, m ₄, r ₁, m ₅, m ₆, m ₇, m ₈, r ₂, m ₉, m ₁₀, m ₁₁, m ₁₂, r ₃, r ₄, r ₅, r ₆, r ₈).

З матриці (*) отримуємо систему перевірних рівнянь, що визначає правила знаходження перевірних елементів:

(**)

Скориставшись системою перевірних рівнянь (**), знаходимо твірну матрицю G _12´20 еквівалентного лінійного блокового коду, яку можна легко привести до канонічного вигляду, розмістивши стовпці, що відповідають перевірним елементам у правій частини твірної матриці, а одиничну підматрицю, що визначає інформаційну частину кодового слова – у лівій:

Закодуємо задану інформаційну послідовність m = (110111000110).

Розмістимо її у вигляді матриці 3´4 і допишемо перевірні елементи до кожного рядка і стовпця:

Þ

Отже, кодовим слово буде (11011110000110001111).

Згідно з умовою задачі на прийомній стороні прийнята послідовність (11011110001110001111). Декодуємо її за ітеративним методом.

Запишемо прийняте слово у вигляді матриці (у даному випадку розмірністю 4´5) і виконаємо перевірку на парність за її кожним рядком і стовпчиком. У разі відсутності помилки контрольні елементи парності за рядками і стовпчиками матриці мають значення 0. Невиконання контролю парності у стовпчику і рядку однозначно визначить координати помилкового елемента – це дозволить його виправити.

Þ

У даному випадку не виконується контроль парності в третьому рядку й першому стовпці, тобто помилковий елемент m [3, 1]. Виправляємо помилку, змінивши значення помилкового елемента на протилежне:

Þ

Отже, виправлена комбінація така:

y= (11011110000110001111).

Декодуємо її, прибравши перевірні елементи:

(11011110000110001111) Þ (110111000110).

Надлишковість коду .

Задачі до розділу 9

1 Нехай X і Y - дискретні випадкові величини, що визначають передавач і приймач дискретних повідомлень. Використовується двійковий симетричний канал, яким передаються повідомлення довжиною 2 біти. Побудувати таблицю ймовірностей прийому.

2 Використовується (8, 9)- код з контролем парності. Оцінити ймовірність того, що цей код не виявить помилкове повідомлення, якщо ймовірність помилки при передачі кожного біта q =1%. Оцініть ймовірність помилкової передачі без використання коду.

3 Задано таблицю кодів деякого коду: 00 ® 00000, 01 ® 01101, 10 ® 10011, 11 ® 11110. Чи є цей код систематичним, лінійним? Записати твірну і перевірну матриці коду. Скільки помилок може виявити і виправити даний код?

4 Завадостійкий код заданий твірною матрицею вигляду

.

Записати всі кодові слова коду. Скільки помилок код може виявити/ виправити? Яка ймовірність невиявлення помилок цим кодом? Як будуть декодовані слова 1001100, 0101011, 0011101?

5 За твірною матрицею

побудувати відповідний (3, 4) - код. Описати основні характеристики коду: мінімальну відстань між кодовими словами, імовірність невиявлення помилки. Побудувати таблицю декодування. Які помилкові ситуації виявляє код?

6 Твірна матриця лінійного блокового коду має вигляд

.

Визначити мінімальну відстань Хеммінга даного коду і кратність помилок, що може виявити/ виправити код. Яка ймовірність невиявлення помилки кодом? Побудувати таблицю декодування. Виправити помилкові комбінації 101110, 010100, 101111.

7 Ітеративний код заданий матрицею вигляду

.

Записати твірну матрицю еквівалентного лінійного блокового коду. Визначити здатність коду виявляти/виправляти помилки, ймовірність невиявлення помилки, якщо ймовірність помилок у каналі q= 10^-4.

8 Закодувати послідовність 110111001 за ітеративним методом. Побудувати перевірну матрицю еквівалентного лінійного блокового коду. Декодувати послідовності 0011000000000111, 0000001111101111, 0101000000000111.

Розділ 10 СПОСОБИ ЗАДАННЯ ЛІНІЙНИХ БЛОКОВИХ КОДІВ. СИНДРОМНЕ ДЕКОДУВАННЯ ЛІНІЙНИХ БЛОКОВИХ КОДІВ

10.1 Способи задання лінійних кодів. Твірна матриця лінійного блокового коду

Найпростіший спосіб задання лінійних кодів – табличний, при якому кожній інформаційній послідовності ставиться у відповідність кодове слово з таблиці кодів. Приклад такого задання коду для послідовностей завдовжки k =3 символи наведений у табл. 3.2.

Таблиця 3.2

Недоліком такого способу подання кодів є те, що при більших k розмір кодової таблиці виявляється дуже великим.

Іншим способом задання лінійних блокових кодів є система перевірних рівнянь, що визначає правила знаходження перевірних символів залежно від інформаційних. Приклад такого задання:

де r₁, r₂, r₃, r₄ - перевірні (контрольні) символи.

Проте найзручнішим і наочним способом задання лінійного блокового коду є його подання за допомогою твірної матриці.

. (3.2)

одинична перевірна

підматриця I_kxk підматриця P_kx(n-k)

u = m ´ G =(m ₁, m ₂, m ₃, m ₄)´ =(m ₁, m ₂, m ₃, m ₄, m ₁+ m ₃+ m ₄, m ₁ + m ₂ + m ₃, m ₂ + m ₃ + m ₄).

Звідси випливає система перевірних рівнянь коду

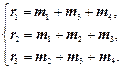
Закодуємо, наприклад, послідовність m= (1011):

(1011)´ =().

10.2 Перевірна матриця лінійного блокового коду

Лінійний блоковий код може бути заданий перевірною матрицеюH_{(n-k) ´ n}, що має таку властивість:

якщо деяка послідовність u є кодовим словом лінійного блокового коду, заданого перевірною матрицею H_{(n-k) ´ n}, то u ´ H ^T = 0, тобто перевірна матриця ортогональна будь-якій кодовій послідовності даного коду.

Перевірна матриця має розмірність (n-k)´ n і таку структуру:

, (3.3)

де - транспонована перевірна підматриця твірної матриці G_{k ´ n}; - одинична підматриця.

З властивості перевірної матриці лінійного блокового коду випливає, що за її допомогою можна визначити, чи є прийнята послідовність кодовим словом даного коду чи ні.

Приклад 2 Для розглянутого прикладу лінійного блокового (4, 7)- коду перевірна матриця матиме вигляд

.

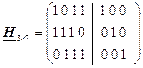Нехай прийнята послідовність y= (1011001). Перевіримо, чи є вона кодовим словом даного коду:

= (1011001) ´ =(1 0 1) ≠ 0.

Отже, послідовність (1011001) не кодове словом даного коду.

10.3 Кодовий синдром і виявлення помилок лінійним блоковим кодом

Нехай u =(u₁, u₂, …, u_n) - кодове слово, передане по каналу з шумом; y =(y₁, y₂, …, y_n) - прийнята послідовність, що через вплив завад може відрізнятися від переданої.

Для описання виникаючих у двійковому симетричному каналі помилок використовується вектор помилоке= (e₁, e₂, …, e_n), що є двійковою послідовністю завдовжки n з одиницями у тих позиціях, де виникли помилки.

Наприклад, вектор помилок е =(0001000) означає однократну помилку у четвертому біті, е= (1100000) - двократну помилку у першому і другому бітах.

При передачі кодового слова u по каналу з шумом прийнята послідовність матиме вигляд y = u + е, де u - передане кодове слово; e – вектор помилок у каналі.

Наприклад: u = (0001000), e= (0001000), тоді y= (0000000).

Щоб перевірити наявність помилок у прийнятій послідовності y, декодер обчислює таку (n-k) - послідовність:

S =(S₁, S₂, …, S_n-k)= y ´ ,

де y - прийнята кодована послідовність; - транспонована перевірна матриця коду.

При цьому у є кодовим словом тоді, коли S=(0 0 … 0), і не є кодовим словом даного коду, якщо S≠0.

Послідовність S є ознакою наявності помилок у прийнятій послідовності y і називається кодовим синдромом.

S = y ´ =(y₁, y ₂, …, y ₇)× 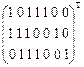=((y₁ + y₃ + y₄+y₅), (y₁ + y₂ + y₃+y₆), (y₂ + y₃ + y₄+y₇)).

Деякі комбінації помилок, використовуючи кодовий синдром, виявити неможливо. Наприклад, якщо передане кодове слово під впливом завад перетвориться на інше кодове слово цього самого коду, то синдром S=y× = 0, і декодер помилок не виявить.

10.4 Синдромне декодування лінійних блокових кодів

Нехай u =(u₁, u₂, …, u_n) - передане кодове слово; е =(е₁, е₂, …, е _n) - вектор помилок; y =(y₁, y₂, … y_n) - прийнята послідовність. Тоді y = u + е.

Date: 2015-11-15; view: 1038; Нарушение авторских прав