
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 6. Однофакторный дисперсионный анализ Краскела-Уоллиса и медианный критерий
|
|
Задание:
Решите следующие задачи, используя однофакторный анализ Краскела-Уоллиса. К этим же задачам примените медианный критерий: сформулируйте и проверьте соответствующие гипотезы. Сравните и прокомментируйте полученные результаты.
1. k групп водителей обучались по различным методикам. После окончания срока обучения был произведен тестовый контроль над случайно отобранными водителями из каждой группы. Получены следующие результаты (задать самостоятельно):
| № группы | Число ошибок, допущенных водителями, 
| Сумма ошибок по каждой группе, 
| Число контролируемых водителей, 
|
| … | |||
| K |
Например:
| № группы | Число ошибок, допущенных водителями, 
| Сумма ошибок по каждой группе, 
| Число контролируемых водителей, 
|
| 1 3 2 1 0 2 1 | |||
| 2 3 2 1 4 – – | |||
| 4 5 3 – – |
На уровне значимости 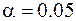 проверить гипотезу об отсутствии влияния различных методик обучения на результаты тестового контроля водителей.
проверить гипотезу об отсутствии влияния различных методик обучения на результаты тестового контроля водителей.
Выполнение работы:
Для выполнения лабораторной работы подготовьте исходные данные для проведения интеллектуального анализа в системе STATISTICA (рис. 4.34).
Гипотеза H 0: выборки получены из одной генеральной совокупности.
В стартовой панели модуля Nonparametric Statistics (Непараметрические статистики) (рис. 4.35) выбираем Kruskal-Wallis ANOVA, median test (Однофакторный дисперсионный анализ Краскела - Уоллиса, медианный критерий) и нажимаем OK.
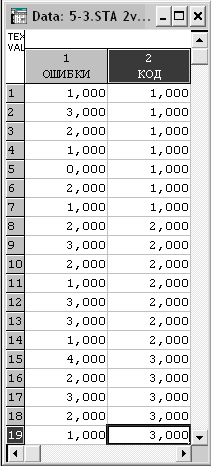
Рис. 4.34. Исходная выборка данных

Рис. 4.35. Стартовая панель модуля Nonparametric Statistics (Непараметрические статистики)
В появившемся окне (рис. 4.36) нажимаем Variables и задаем переменные (рис. 4.37). Нажимаем OK (рис. 4.38).

Рис. 4.36. Окно Kruskal-Wallis ANOVA, median test (Однофакторный дисперсионный анализ Краскела - Уоллиса, медианный критерий)

Рис. 4.37. Окно выбора переменных
В появившемся окне Kruskal-Wallis ANOVA, median test (Однофакторный дисперсионный анализ Краскела - Уоллиса, медианный критерий) нажимаем Codes (рис. 4.38) и выбираем коды для группируемых переменных (рис. 4.39). Нажимаем OK и получаем следующую таблицу результатов (рис. 4.40).

Рис. 4.38. Окно Kruskal-Wallis ANOVA, median test (Однофакторный дисперсионный анализ Краскела - Уоллиса, медианный критерий)

Рис. 4.39. Окно выбора кодов

Рис. 4.40. Таблица результатов анализа
Критерий Краскела-Уоллиса служит для проверки гипотезы H 0: k выборок объемов n 1, …, nk получены из одной генеральной совокупности.
Гипотеза H 0 принимается на уровне значимости a, если выборочное значение Н в статистики H удовлетворяет условию:
 .
.
Так как квантиль распределения c2:  , а выборочное значение статистики H: H в = 2.75, то можно сделать вывод: гипотеза H 0 принимается, т. е. разные методики не влияют на результат обучения.
, а выборочное значение статистики H: H в = 2.75, то можно сделать вывод: гипотеза H 0 принимается, т. е. разные методики не влияют на результат обучения.
Применим для данной задачи медианный критерий (рис. 4.41), который используется для проверки гипотезы H 0: все k генеральных совокупностей имеют равные медианы.
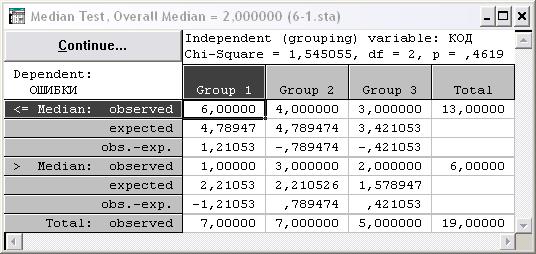
Рис. 4.41. Таблица результатов медианного теста
Вывод: если гипотеза H 0 верна, статистика c2 имеет распределение хи-квадрат с k – 1 числом степеней свободы. Гипотеза H 0 отклоняется, если
 .
.
В данном случае:  , а
, а  . Следовательно, гипотеза H 0 принимается.
. Следовательно, гипотеза H 0 принимается.
И в том и в другом случае гипотеза принимается, следовательно, разные методики не влияют на результаты обучения.
2. Инвестор хочет знать, существуют ли значительные различия в доходах от акций, облигаций и инвестиционных фондов. Он взял случайные выборки каждого способа вложения капиталов и получил следующие результаты (задать самостоятельно):
| Доходы (в %) | |||||||
| Акции | |||||||
| Облигации | |||||||
| Инвестиционные фонды |
Например:
| Доходы (в %) | |||||||
| Акции | 2.0 | 6.0 | 2.0 | 2.1 | 6.2 | 2.9 | 3.0 |
| Облигации | 4.0 | 3.1 | 2.2 | 5.3 | 5.9 | 5.5 | |
| Инвестиционные фонды | 3.5 | 3.1 | 2.9 | 6.0 | 4.5 | 3.2 |
- определите основную H 0 и альтернативную H 1 гипотезы;
- проверьте гипотезу H 0 при 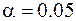 ;
;
- сформулируйте окончательный вывод.
Date: 2015-11-15; view: 1434; Нарушение авторских прав