
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 5. Критерий Манна-Уитни
|
|
Задание:
Решите следующие задачи, используя критерий серий Вальда-Вольфовица и Манна-Уитни. Сравните и прокомментируйте результаты.
1. По выборкам из 2-х партий микросхем после операции легирования поликремния измерялось удельное сопротивление. Результаты замеров следующие (задаете самостоятельно):
| … | n | |||||||||||
| 1-я партия | ||||||||||||
| 2-я партия |
Например:
| 1-я партия | 52.2 | 32.5 | 49.5 | 32.5 | 191.5 | 112.5 | 69.1 | 48.5 | 16.5 | |
| 2-я партия | 17.5 | 43.5 | 90.5 | – | – |
Можно ли утверждать, что обе партии получены из одной генеральной совокупности? Принять  .
.
Выполнение работы:
Для выполнения лабораторной работы подготовьте исходные данные для проведения интеллектуального анализа в системе STATISTICA (рис. 4.27).
Гипотеза H 0: выборки получены из одной генеральной совокупности.
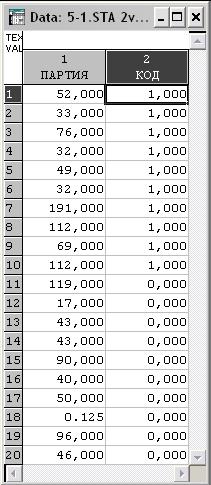
Рис. 4.27. Исходная выборка данных
Решение задачи с использованием критерия серий Вальда-Вольфовица:
По аналогии с предыдущей задачей производим все необходимые действия и получаем следующую таблицу результатов (рис. 4.28):

Рис. 4.28. Таблица результатов анализа
Вывод: выборочное значение Z: ze» 0.46.
Так как это значение меньше квантили распределения N (0, 1) u 0.99 = 2.326, то гипотеза H 0 не отклоняется, т. е. обе выборки получены из одной генеральной совокупности.
Решение задачи с использованием критерия Манна-Уитни:
В стартовой панели модуля Nonparametric Statistics (Непараметрические статистики) (рис. 4.29) выбираем Mann-Whitney U test (Критерий Манна - Уитни) и нажимаем OK.
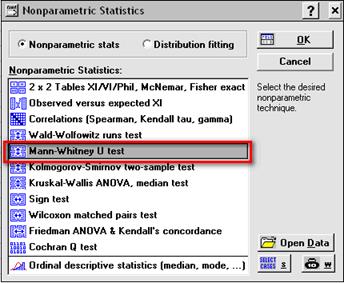
Рис. 4.29. Стартовая панель модуля Nonparametric Statistics (Непараметрические статистики)
В появившемся окне (рис. 4.30) нажимаем Variables и задаем переменные (рис. 4.31). Нажимаем OK (рис. 4.32).

Рис. 4.30. Окно Mann-Whitney U Test (Критерий Манна - Уитни)
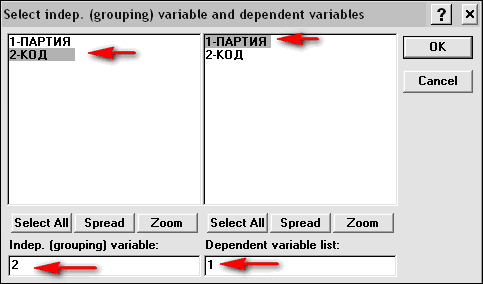
Рис. 4.31. Окно выбора переменных
В появившемся окне Mann-Whitney U Test (Критерий Манна - Уитни) выполняем соответствующие установки (рис. 4.32), нажимаем OK и получаем следующую таблицу результатов (рис. 4.33).
Вывод: для проверки гипотезы H 0 используется статистика Z. Выборочное значение этой статистики 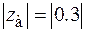 . Это значение сравнивается с квантилью стандартного нормального распределения
. Это значение сравнивается с квантилью стандартного нормального распределения  . Так как
. Так как  , то гипотеза H 0 не отклоняется, т. е. обе партии получены из одной генеральной совокупности.
, то гипотеза H 0 не отклоняется, т. е. обе партии получены из одной генеральной совокупности.
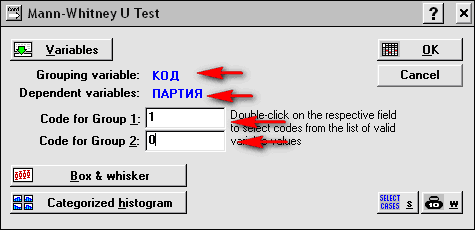
Рис. 4.32. Окно Mann-Whitney U Test (Критерий Манна - Уитни)

Рис. 4.33. Таблица результатов анализа
2. Профессор решил определить, быстрее или медленнее его наиболее способные студенты сдают письменные тесты: быстрее потому, что они быстрее вспоминают усвоенные навыки или медленнее потому, что на запись всего, что они знают, уходит больше времени. При решении задач по физике он записал полученные студентами оценки в порядке сдачи их работ (количество студентов и результаты работ задать самостоятельно):
Например:
| Порядок сдачи работ | Оценки | |||||||||
| 1-10 | ||||||||||
| 11-20 | ||||||||||
| 21-30 |
Студентов, набравших 90 и более баллов, профессор считает наиболее способными студентами. Может ли он при уровне значимости 5% считать, что сдача работ студентами носила случайный характер?
Можно ли считать, что студенты, набравшие 60 или более баллов, которые считаются прошедшими тест, сдали свои работы в случайной последовательности в отличие от тех, кто не прошел тест? Уровень значимости 5%.
3. Для контроля настройки 2-х станков-автоматов, производящих детали по одному чертежу, определили отклонения от номинальных размеров у некоторых деталей, изготовленных на обоих станках. В результате получили следующие данные (в мкм.) (задать самостоятельно):
| … | 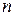
| |||||||||||
| Станок A | ||||||||||||
| Станок B |
Например:
| Станок A | -14 | -50 | -35 | -8 | -20 | |||||||
| Станок B | -49 | -35 | -48 | -45 | -59 | -19 |
Проверить гипотезу H 0 о том, что отклонения от номинальных размеров на обоих станках в среднем не отклоняется на уровне значимости  .
.
Date: 2015-11-15; view: 2378; Нарушение авторских прав