Выполнение работы

Для выполнения лабораторной работы подготовьте исходную выборку данных (один результативный признак Y, пять факторных признаков X_i) для проведения интеллектуального анализа в системе STATISTICA (рис. 3.1).

Рис. 3.1. Исходная выборка данных

Для проведения регрессионного анализа на панели инструментов нажимаем на кнопку переключателя модулей STATISTICA Module Switcher (рис. 3.2).

Рис. 3.2. Переключатель модулей Module Switcher

В появившемся окне (рис. 3.3) выбираем модуль Multiple Regression (Множественная регрессия), нажав кнопку Switch to (Переключиться в) или просто дважды щелкнув мышью по названию модуля Multiple Regression.

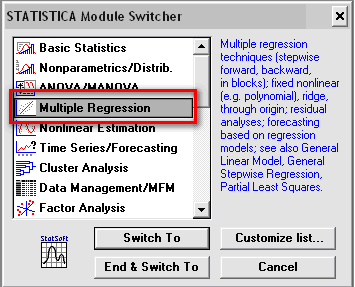
Рис. 3.3. Окно Переключателя модулей Module Switcher

На экране появится стартовая панель модуля (рис. 3.4) Multiple Regression (Множественная регрессия), где задаются зависимая (Y) и независимые переменные (X ₁- X ₅).

Рис. 3.4. Окно модуля Multiple Regression

Чтобы выполнить пошаговую регрессию нужно снять все ограничения (рис. 3.5) и нажать OK.

Рис. 3.5. Окно модуля Multiple Regression

Процедура пошаговой регрессии Backward stepwise:

В появившейся панели Model Definition (Задание модели) выполняем следующие установки (рис. 3.6) и нажимаем ОК.

Рис. 3.6. Установки регрессионной модели

Процедура пошаговой регрессии на нулевом шаге:

В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.7) нажимаем Regression summary и получаем результат регрессии на нулевом шаге (рис. 3.8).

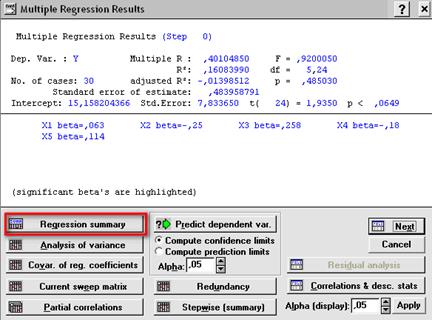
Рис. 3.7. Окно результатов регрессионного анализа

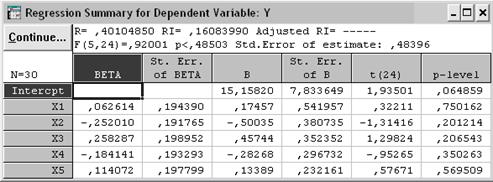
Рис. 3.8. Результаты регрессионного анализа на нулевом шаге

Вывод: наименьшее значение t -статистики имеет переменная X ₁, следовательно, коэффициент b незначим, переменная X ₁ исключается из дальнейшего анализа.

Нажимаем кнопку Continue, и в появившемся окне (рис. 3.9) нажимаем кнопку Next, получаем результат пошаговой регрессии на следующем шаге (рис. 3.10):

Рис. 3.9. Окно результатов регрессионного анализа

Рис. 3.10. Результаты регрессионного анализа на первом шаге

Вывод: из рассмотрения исключается переменная X ₅.

Нажимаем кнопку Continue, и в появившемся окне (рис. 3.12) нажимаем кнопку Next, получаем результат пошаговой регрессии на следующем шаге (рис. 3.13).

Рис. 3.12. Окно результатов регрессионного анализа

Рис. 3.13. Результаты регрессионного анализа на втором шаге

Вывод: получаем следующее уравнение регрессии:

.

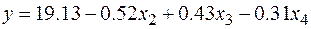В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.14) нажимаем Stepwise summary и получаем результаты выполнения процедуры по шагам (рис. 3.15).

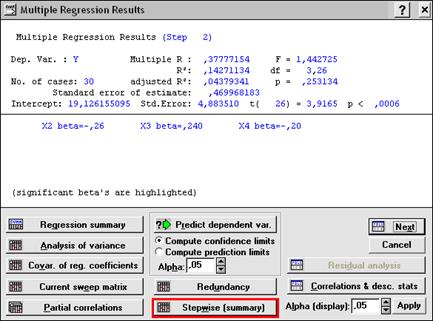
Рис. 3.14. Окно результатов регрессионного анализа

Рис. 3.15. Результаты выполнения процедуры по шагам

Процедура пошаговой регрессии Forward stepwise:

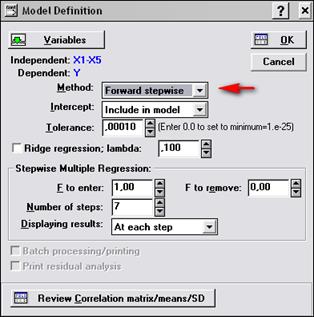
Рис. 3.16. Установки регрессионной модели

Данная процедура организована в обратном направлении по сравнению с предыдущей процедурой удаления переменных.

В появившейся панели Model Definition (Задание модели) выполняем необходимые установки (рис. 3.16) и нажимаем ОК.

В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.17) нажимаем Regression summary и получаем результат регрессии на нулевом шаге.

Рис. 3.17. Окно результатов регрессионного анализа

Нажимаем кнопку Next, получаем результат пошаговой регрессии на следующем шаге (рис. 3.18-3.19).

Рис. 3.18. Окно результатов регрессионного анализа

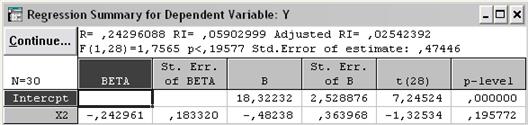
Рис. 3.19. Результаты регрессионного анализа на первом шаге

Нажимаем кнопку Continue и в появившемся окне (рис. 3.20) нажимаем кнопку Next, после чего получаем результат пошаговой регрессии на следующем шаге (рис. 3.21).

Рис. 3.20. Окно результатов регрессионного анализа

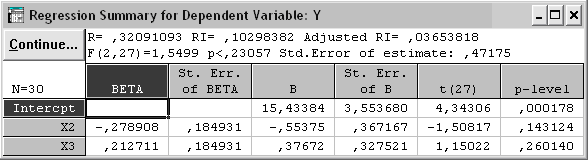
Рис. 3.21. Результаты регрессионного анализа на втором шаге

Нажимаем кнопку Continue и в появившемся окне (рис. 3.22) нажимаем кнопку Next, после чего получаем результат пошаговой регрессии на следующем шаге (рис. 3.23).

Вывод: получаем следующее уравнение регрессии:

.

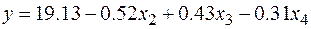В появившемся окне Multiple Regression Results (Результаты множественной регрессии) нажимаем Stepwise summary и получаем результаты выполнения процедуры по шагам (рис. 3.24).

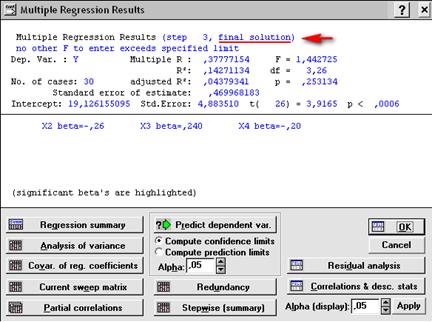
Рис. 3.22. Окно результатов регрессионного анализа

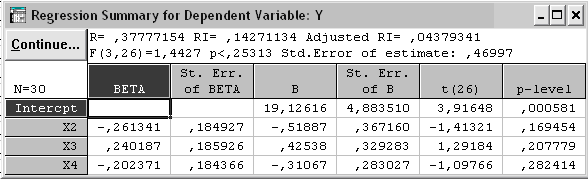
Рис. 3.23. Результаты регрессионного анализа на третьем шаге

Рис. 3.24. Результаты выполнения процедуры по шагам

Вывод: На первом шаге в уравнение регрессии включается фактор, имеющий наибольший коэффициент корреляции с y; определяется уравнение простой линейной регрессии и определяется значимость, на последующих шагах происходит та же процедура, до того момента пока не будут выбраны все значимые коэффициенты.

Таким образом, результаты Forward stepwise и Backward stepwise совпадают, следовательно, уравнение регрессии имеет вид:

.

Для построения корреляционной матрицы в окне Multiple Regression Results (Результаты множественной регрессии) нажимаем Correlations & desc. stats. (рис. 3.25), в появившемся окне (рис. 3.26) нажимаем Correlations (Корреляция) и получаем корреляционную матрицу (рис. 3.27).

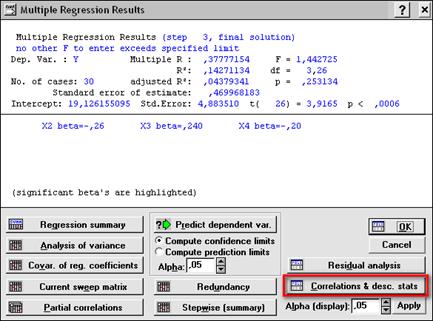
Рис. 3.25. Окно результатов регрессионного анализа

Рис. 3.26. Окно описательных статистик

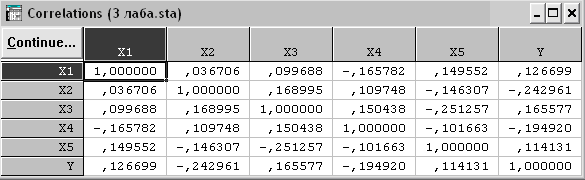
Рис. 3.27. Корреляционная матрица

Результаты регрессионного анализа:

В появившейся панели Model Definition (Задание модели) выполняем следующие установки (рис. 3.28) и нажимаем ОК.

В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.29) нажимаем Regression summary и получаем результат регрессии на нулевом шаге (рис. 3.30).

Уравнение множественной регрессии имеет вид:

.

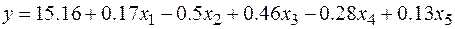Из таблицы видно, что переменная X ₁ исключается из дальнейшего анализа, так как коэффициент регрессии b₁ незначим (t (24) = 0.322 и p - level = 0.75).

В появившейся панели Model Definition (Задание модели) выполняем следующие установки (рис. 3.31) и нажимаем ОК.

В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.32) нажимаем Regression summary и получаем результат регрессии на первом шаге (рис. 3.33).

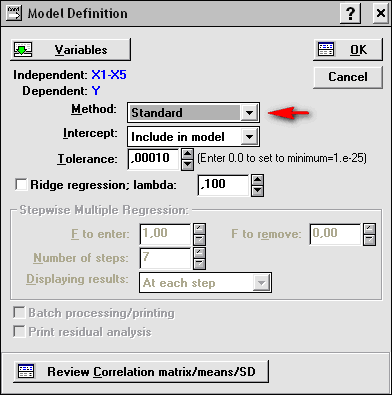
Рис. 3.28. Установки регрессионной модели

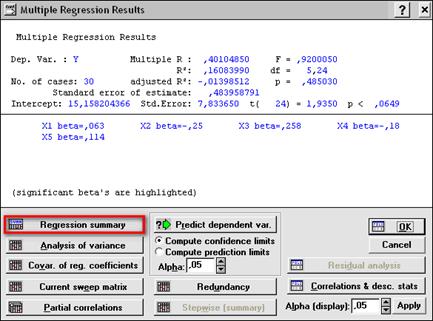
Рис. 3.29. Окно результатов регрессионного анализа

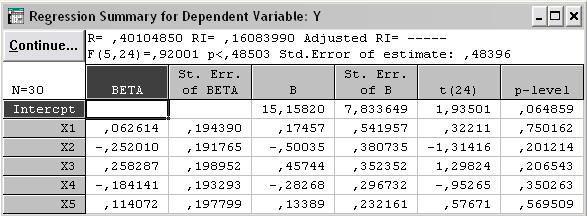
Рис. 3.30. Результаты регрессионного анализа на нулевом шаге

Рис. 3.31. Установки регрессионной модели

Уравнение множественной регрессии имеет вид:

.

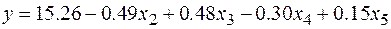Далее из рассмотрения исключается переменная X ₅ (t (25) = 0.656 и p - level = 0.518).

В появившейся панели Model Definition (Задание модели) выполняем следующие установки (рис. 3.34) и нажимаем ОК.

Рис. 3.32. Окно результатов регрессионного анализа

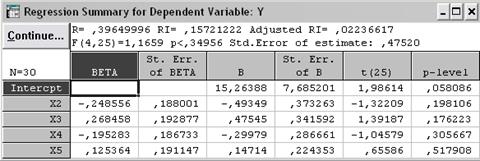
Рис. 3.33. Результаты регрессионного анализа на первом шаге

В появившемся окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.34) нажимаем Regression summary и получаем результат регрессии на первом шаге (рис. 3.35).

Рис. 3.34. Установки регрессионной модели

Рис. 3.35. Окно результатов регрессионного анализа

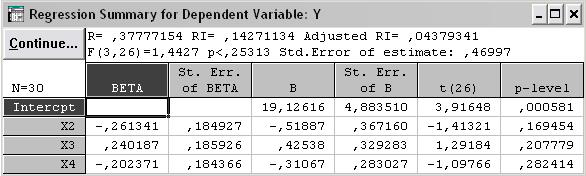
Рис. 3.36. Результаты регрессионного анализа на втором шаге

Следовательно, уравнение множественной регрессии имеет вид: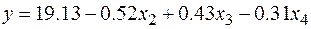

Дисперсионный анализ:

Для проведения дисперсионного анализа в окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.37) нажимаем Analysis of variance (Дисперсионный анализ) и получаем результаты в соответствующей таблице (рис. 3.38), где Regress – сумма квадратов, обусловленная регрессией ; Residual – остаточная сумма квадратов 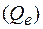; Total – сумма квадратов отклонений зависимой переменной Y от среднего .

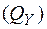Рис. 3.37. Окно результатов регрессионного анализа

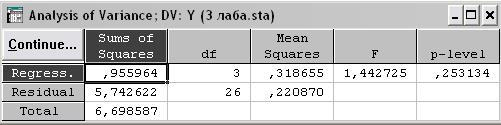
Рис. 3.38. Результаты дисперсионного анализа

Вывод: из таблицы видно что, F = 1.44, что подтверждает значимость модели.

Для подтверждения предположения регрессионного анализа и адекватности модели, произведем анализ остатков. Для этого в окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.39) нажимаем Residual analysis (Анализ остатков). В появившемся окне выбираем критерий Дарбина-Уотсона (рис. 3.40) и получаем результаты в соответствующей таблице (рис. 3.41).

В данном случае статистика Дарбина-Уотсона d = 2.23, что больше табличного значения d = 1.49, следовательно, гипотеза: все сериальные корреляции равны нулю, принимается.

Рис. 3.40. Окно результатов регрессионного анализа

Рис. 3.40. Окно Residual analysis (Анализ остатков)

Рис. 3.41. Результаты анализа остатков

Чтобы посмотреть остатки и их графики произведем следующие действия. В окне Residual analysis (Анализ остатков) выбираем Plots of residuals (рис. 3.42) и получаем график остатков и их значения в соответствующей таблице (рис. 3.43).

Все остатки укладываются в симметричную относительно нулевой линии полосу шириной ±2 S, следовательно, дисперсии ошибок наблюдений постоянны.

Рис. 3.42. Окно Residual analysis (Анализ остатков)

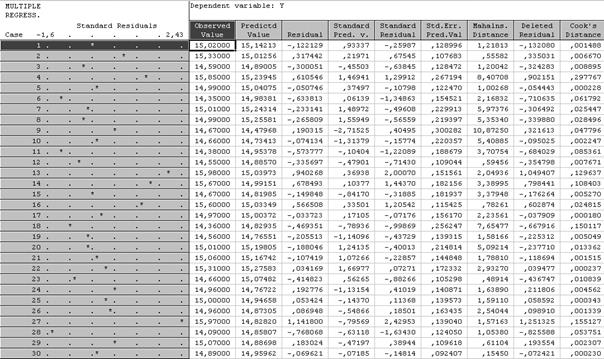
Рис. 3.43. Остатки и их значения

Проверим гипотезу о нормальности распределения остатков. Для этого в окне Residual analysis (Анализ остатков) выбираем Normal plot of resids (рис. 3.44) и получаем график распределения остатков относительно графика регрессионной модели (рис. 3.45).

Рис. 3.44. Окно Residual analysis (Анализ остатков)

Рис. 3.45. Остатки и график регрессионной модели

Вывод: из графика видно, что точки расположены близко к прямой, следовательно, остатки распределены по нормальному закону. Таким образом, предположения регрессионного анализа выполняются. Регрессионная модель адекватна результатам наблюдений и может использоваться для прогнозирования.

Вычисление предсказанных значений доверительных интервалов:

Вычисления проводятся при нажатии кнопки Predict dependent var (Прогнозирование значения зависимой переменной) в окне Multiple Regression Results (Результаты множественной регрессии) (рис. 3.46), предварительно задав уровень значимости и вид вычисляемого доверительного интервала (для среднего предсказанного значения). Результаты вычисления предсказанных значений доверительных интервалов приведены в соответствующей таблице (рис. 3.47).

Рис. 3.46. Окно результатов регрессионного анализа

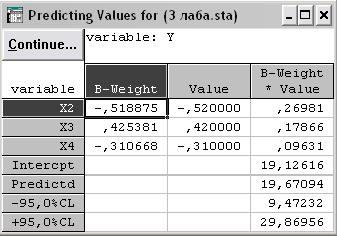
Рис. 3.47. Результаты вычисления предсказанных значений доверительных интервалов

Date: 2015-11-15; view: 564; Нарушение авторских прав