Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Основные формулы. 4.1. Момент силы относительно неподвижной точки:
|
|
4.1. Момент силы относительно неподвижной точки:
где 
– радиус вектор точки приложения силы 
.
4.2. Момент силы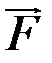 
, действующей на тело, относительно оси вращения:
,
где 
– плечо силы 
(кратчайшее расстояние от оси вращения до линии действия силы) и
где r– расстояние от оси вращения до точки приложения силы, 
– угол между направлением действия силы и радиус–вектором 
, проведенным от оси вращения к точке приложения силы.
4.3. Момент инерции:
- материальной точки 
- твердого тела 
где 
– расстояние элемента массы 
от оси вращения.
То же в интегральной форме: 
4.4. Теорема Штейнера. Момент инерции тела J относительно произвольной оси равен:
,
где J 0– момент инерции этого тела относительно оси, проходящей через центр тяжести параллельно заданной оси, а – расстояние между осями, m – масса тела.
Таблица4.1.Момент инерции некоторых тел правильной геометрической формы.
| Тело и ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой m и длиной l | |
| a) ось проходит через центр тяжести стержня перпендикулярно к стержню | 
|
| б) ось проходит через конец стержня перпендикулярно к стержню. | 
|
| Тонкое кольцо, обруч, труба радиусом R и массой m; маховик радиусом R и массой m, распределенной по ободу. Ось проходит через центр перпендикулярно к плоскости основания. |
|
| Круглый однородный диск (цилиндр) радиусом R и массой m. Ось проходит через центр диска перпендикулярно к плоскости основания. | 
|
| Однородный шар массой m и радиусом R. Ось проходит через центр шара. | 
|
4.5. Момент импульса материальной точки относительно не подвижной точки:
или 
где m – масса точки, 
– линейная скорость точки, r – расстояние точки от оси, относительно которой определяется момент импульса, 
–импульс материальной точки.
4.6. Момент импульса твёрдого тела относительно не подвижной оси:
где 
– момент инерции тела относительно оси 
; 
– угловая скорость вращения.
4.7. Основное уравнение динамики вращательного движения:
; 
,
где 
– угловое ускорение.
Date: 2015-11-13; view: 1105; Нарушение авторских прав