
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Диаграммы Карно
|
|
Данный метод состоит в том, чтобы занести логическое выражение, подлежащее упрощению, в сетку двух, трех, четырех, пяти и, возможно, шести переменных. Когда логическое выражение занесено в диаграмму Карно, оно упрощается графическими методами.
Диаграммой Карно называется сетка (решетка) содержащая некоторое число пустых клеток, количество которых равно числу комбинаций переменных логической функции, подлежащей упрощению.
Диаграмма двух переменных A и B будет содержать четыре клетки:
| A | |||
| B | |||
Диаграмма трех переменных A, B и C будет содержать восемь клеток:
| AB | |||||
| C | |||||
Диаграмма четырех переменных A, B, C и D будет содержать уже шестнадцать клеток, поскольку число клеток определяется как степень двойки от числа переменных:
| AB | |||||
| CD | |||||
В случае размещения двух переменных по одной стороне диаграммы, порядок следования их комбинаций должен быть таким, чтобы при переходе от одной клетки к другой соседней клетке только одна переменная меняла свое значение, а именно: 00, 01, 11, 10. Этот порядок всегда должен соблюдаться для избежания серьезных ошибок.
Для того, чтобы занести логическую функцию в диаграмму Карно, необходимо поместить единицы в клетки, соответствующие комбинациям переменных, на которых функция равна единице.
Пусть, например, необходимо занести в диаграмму Карно функцию четырех переменных:

| AB | |||||
| CD | |||||
Первый терм  дает единицу в клетке, для которой A = 0, B = 1, C = 0 и D = 1, т. е. в клетке, находящейся на пересечении второй строки и второго столбца. Второй терм
дает единицу в клетке, для которой A = 0, B = 1, C = 0 и D = 1, т. е. в клетке, находящейся на пересечении второй строки и второго столбца. Второй терм  дает две единицы в клетках, для которых A = 1, B = 1, C = 0, а значение D безразлично, т. е. может быть равно как нулю, так и единице. Данные комбинации соответствуют клеткам, находящимся на пересечении третьего столбца и первой и второй строк. Третий терм
дает две единицы в клетках, для которых A = 1, B = 1, C = 0, а значение D безразлично, т. е. может быть равно как нулю, так и единице. Данные комбинации соответствуют клеткам, находящимся на пересечении третьего столбца и первой и второй строк. Третий терм  даст четыре единицы в клетках, для которых A = 0, D = 1, а значения B и C могут быть равны как нулю, так и единице, что соответствует клеткам, находящимся на пересечении первого и второго столбцов и второй и третьей строк. На остальных комбинациях функция равна нулю, поэтому в оставшиеся клетки вносится значение 0.
даст четыре единицы в клетках, для которых A = 0, D = 1, а значения B и C могут быть равны как нулю, так и единице, что соответствует клеткам, находящимся на пересечении первого и второго столбцов и второй и третьей строк. На остальных комбинациях функция равна нулю, поэтому в оставшиеся клетки вносится значение 0.
После занесения булевой функции в диаграмму Карно, приступают к ее чтению. При этом функция будет упрощаться, если сгруппировать единицы, находящиеся в соседних клетках. Под соседними клетками понимают две клетки диаграммы Карно, для которых имеется различие в значении только одной единственной переменной.
Каждый раз, когда имеются хотя бы две соседние клетки, содержащие единицы, функция, представленная в диаграмме Карно, может быть упрощена. При чтении функции единицы соседних клеток заключаются в замкнутый контур, что означает, что эти единицы сгруппированы вместе для получения упрощенного выражения функции. В одной и той же диаграмме может существовать множество соседних единиц. В этом случае организуют множество контуров и записывают сумму полученных упрощенных термов. Имеется возможность получения наиболее простого решения, т. е. содержащего минимум логических переменных для рассматриваемой функции, заключая в контур максимум соседних клеток. Для этого контуры делают максимально возможно большими.
Пусть, например, необходимо записать аналитическое выражение логической функции, представленной в заданной диаграмме:
| AB |  III III
| ||||
| CD | |||||
 1 1
| |||||
 1 1
| |||||
 1 1
| |||||
| III |
Заключая единицы в соседних клетках в три контура, получают следующее логическое выражение:

Использование диаграмм Карно представляет собою элегантный и эффективный метод упрощения логических схем. Он состоит в следующем: на основании определенной логической схемы записывается логическое выражение выхода, выраженное в функциях входных переменных, затем выражение, занесенное в диаграмму Карно, упрощается методом контуров, рассмотренным выше, и на основании полученного выражения создается новая схема.
Пусть, например, необходимо упростить логическую схему, представленную на рис. 4.1.
В соответствии с этой схемой логическое выражение, описывающее ее выход, будет иметь следующий вид:

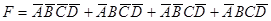 и
и 
Занесем значение функции  в соответствующую диаграмму Карно:
в соответствующую диаграмму Карно:
 AB AB
| I | ||||
| CD | |||||
 0 0
| |||||
 0 0
| |||||
 1 1
| |||||
| I |
После упрощения мы получим следующее значение функции:

и для функции  , заключая в контуры нули диаграммы, получим:
, заключая в контуры нули диаграммы, получим:

Откуда получим схему, представленную на рис. 4.2., эквивалентную схеме рисунка 4.1.
 Можно заметить, что схема рисунка 4.2. значительно экономичнее схемы рисунка 4.1.
Можно заметить, что схема рисунка 4.2. значительно экономичнее схемы рисунка 4.1.
Date: 2015-11-13; view: 542; Нарушение авторских прав